Question

A hollow cylindrical furnace of length $l=2m$ has inner radius $r_1 = 50$ cm and outer radius $r_2 = 1m$. The furnace is made up of a metal having thermal conductivity $400 Wm^{-1}K^{-1}$. The inner curved surface of furnace is maintained at temperature $1300^\circ C$ by burning coal at a uniform rate. If the temperature of surrounding is $40^\circ C$ and 1 kg coal releases $30 \times 10^6 J$ on burning then the amount of coal required per second to maintain the temperature of furnace is $100n$ grams. Find $n$. (Take $\pi^2 = 0.7$ and $\pi \approx \frac{25}{8}$)

Answer 1

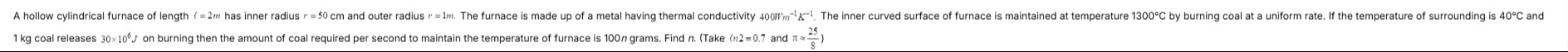
3

Answer 2

Solution:

1. Heat conduction in a cylindrical shell:

   $$Q = \frac{2\pi k l (T_1-T_2)}{\ln(r_2/r_1)}$$

   where $k = 400\, \text{W/m·K},$ $l = 2\, \text{m},$ $T_1 = 1300^\circ \text{C},$ $T_2 = 40^\circ \text{C}$ (so, $\Delta T = 1260\,K$), $r_1 = 0.5\, \text{m},$ $r_2 = 1\, \text{m}.$

2. Approximations given:

   $\ln(r_2/r_1)= \ln(2)\approx 0.7$ and $\pi\approx \frac{25}{8}$.

3. Substitute values:

   $$Q = \frac{2\left(\frac{25}{8}\right) \times 400 \times 2 \times 1260}{0.7}$$

   First, calculate $2\pi$:

   $$2\pi = 2\times\frac{25}{8} = \frac{50}{8} = 6.25$$

   Then,

   $$Q = \frac{6.25\times400\times2\times1260}{0.7}$$ $$= \frac{6.25 \times 400 \times 2 \times 1260}{0.7} = \frac{6.25 \times 400 \times 2520}{0.7}$$

   Calculate step by step:

   $$6.25 \times 400 = 2500, \quad 2500 \times 2 = 5000, \quad 5000 \times 1260 = 6,300,000.$$

   Thus,

   $$Q = \frac{6,300,000}{0.7} = 9,000,000\, \text{W}.$$

4. Coal energy balance:

   Each kg of coal releases $30 \times 10^6\, \text{J}.$ Therefore, the mass of coal required per second:

   $$\text{Coal per second} = \frac{9\times10^6}{30\times10^6} = 0.3\, \text{kg/s}.$$

   Converting to grams:

   $$0.3\, \text{kg/s} = 300\, \text{grams/s}.$$

   We are told that this equals $100n$ grams per second, so:

   $$100n = 300 \quad \Longrightarrow \quad n = 3.$$

Summary:

• Core Explanation: Used conduction formula for a cylindrical shell to compute $Q$. Then, computed the coal consumption using energy provided per kg of coal and equated $300$ grams/s to $100n$ grams.

• Answer: $n = 3$.