Question

A hollow cylindrical box of length $1m$ and area of cross-section $25c{m^2}$ is placed in a three dimensional coordinate system as shown in the figure. The electric field in the region is given by $E = 50x\hat i$ , where $E$ is in $N{C^{ - 1}}$ and $x$ is in meters.

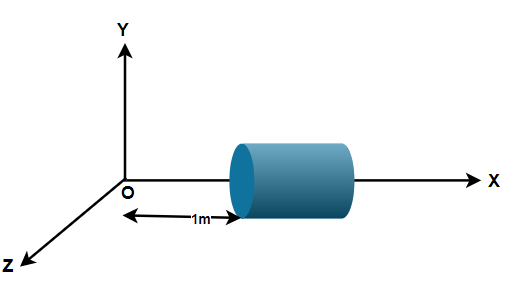
Find
$\left( i \right)$ Net flux through the cylinder
$\left( {ii} \right)$ Charge enclosed by the cylinder

Answer 1

So in this question, we have to find the electric flux and for this, we have the formula for flux given by $\vec E \cdot \vartriangle \vec S$ . By using this formula we will find the electric flux. For finding the enclosed charge we will use the gauss formula, which is given by $\oint {\vec E \cdot d\vec S} = \dfrac{q}{{{\varepsilon _ \circ }}}$ . So by using this we will get the enclosed charge.
Formula used:
Gauss’s law,
${\phi _E} = \oint {\vec E \cdot d\vec S} = \dfrac{q}{{{\varepsilon _ \circ }}}$
Here, ${\phi _E}$ will be the electric flux through a closed surface and enclosing volume.
$q$ , will be the total charge.
${\varepsilon _ \circ }$ , is the electric constant.

Complete step by step answer: So we have the area of cross-section given as
$\vartriangle S = 25c{m^2} = 25 \times {10^{ - 4}}{m^2}$
$\left( i \right)$ Since, from the question it is clear that the electric field is only along the x-axis, therefore the flux will pass through the cross-section of the cylinder.

Hence, the magnitude of electric field at cross-section $A$,
$\Rightarrow {E_A} = 50 \times 1 = 50N/C$
Similarly, the magnitude of electric field at cross-section $B$,
$\Rightarrow {E_B} = 50 \times 2 = 100N/C$
Therefore, the electric flux will become
$\Rightarrow \oint {{\phi _A} = \vec E \cdot \vartriangle \vec S}$
And on substituting the values, we get
$\Rightarrow \oint {{\phi _A} = 50 \times 25 \times {{10}^{ - 4}} \times \cos {{180}^ \circ }}$
And on solving it, we get
$\Rightarrow \oint {{\phi _A} = - 0.125N{m^2}/{C^2}}$
Similarly for $B$ also, it will be
$\Rightarrow \oint {{\phi _B} = \vec E \cdot \vartriangle \vec S}$
And on substituting the values, we get
$\Rightarrow \oint {{\phi _B} = 100 \times 25 \times {{10}^{ - 4}} \times \cos {0^ \circ }}$
And on solving it, we get
$\Rightarrow \oint {{\phi _B} = 0.25N{m^2}/{C^2}}$
Therefore, the net flux through the cylinder will be equals to
$\Rightarrow \oint {\phi = } \,\,\oint {{\phi _A}} + \oint {{\phi _B}}$
And on substituting the values, we get
$\Rightarrow \oint {\phi = } \,\,0.125 + 0.25$
And on solving it, we get
$\Rightarrow \oint {\phi = } \,\,0.375N{m^2}/{C^2}$
Therefore, the net flux through the cylinder is equal to $0.375N{m^2}/{C^2}$ .
$\left( {ii} \right)$ Now by using the Gauss’s law, we have
$\phi = \oint {\vec E \cdot d\vec S} = \dfrac{q}{{{\varepsilon _ \circ }}}$
Now on substituting the values, we get
$\Rightarrow 0.375 = \dfrac{q}{{8.85 \times {{10}^{ - 12}}}}$
And on solving it, we get
$\Rightarrow q = 8.85 \times {10^{ - 12}} \times 0.375$
And on solving,
$\Rightarrow q = 3.3 \times {10^{ - 12}}C$

Therefore, the charge enclosed by the cylinder equals $3.3 \times {10^{ - 12}}C$ .

Note: The final goal of Gauss’s law in electrostatics is to calculate the electric field for a given charge distribution, surrounded by a closed surface. The purpose of the electric field becomes much modest if the body due to a closed surface shows some symmetry in relation to the given charge distribution.