Question

A hollow cylinder of radius $R$ is rotated about its axis which is kept vertical. Calculate the minimum frequency of revolution such that a body kept inside of the wall does not slip down. The coefficient of friction between the body and surface of the cylinder is $\mu$.
A. $\dfrac{1}{{2\pi }}\sqrt {\dfrac{g}{{\mu R}}}$
B. $\dfrac{1}{{2\pi }}\sqrt {\dfrac{{\mu g}}{R}}$
C. $2\pi \sqrt {\dfrac{{\mu g}}{R}}$
D. $2\pi \sqrt {\dfrac{R}{{\mu g}}}$

Answer 1

We'll employ the concept of centrifugal force operating on the body inside the cylinder since the cylinder is rotating. They will have friction between them, so we will use the friction force equation, and it will circle with a certain frequency, so we will use the angular frequency formula. To keep the body from slipping, compare these equations and find the desired minimum frequency of revolution.

Formula used:
Centrifugal force, $N = m{\omega ^2}r$
where $N$ is the centrifugal force, $m$ is the mass, $\omega$ is the angular velocity, $r$ is the radius.
Frictional force, $f = \mu N$
where $f$ is the friction force, $\mu$ is the coefficient of friction, $N$ is the normal force.
Angular frequency, $\omega = 2\pi f$
where $\omega$ is the angular frequency, $f$ is the frequency.

Complete step by step answer:

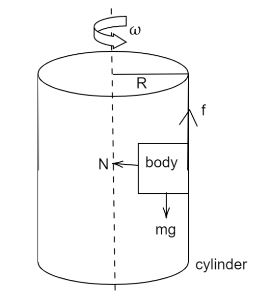
We have been given a hollow cylinder of radius $R$ inside which a body is kept. We have to find the minimum frequency of revolution with which the cylinder should revolve so that the body does not fall. Let the frequency of the cylinder be $f'$ , the mass of the body be $m$. Now forces acting on the body are $mg$ which is in a downward direction due to gravity, frictional force $f$ in an upward direction to balance $mg$ and normal force perpendicular to the block.

Since the cylinder is rotating the block inside the cylinder experiences centrifugal force in the outward direction which provides the normal $N$. Therefore,
$N = m{\omega ^2}R$
And $f = mg$
The frictional force is $f = \mu N$
So, $\mu N = mg$
Putting the value of $N$ in the above equation.
$\Rightarrow \mu m{\omega ^2}R = mg$
$\Rightarrow \mu = \dfrac{g}{{{\omega ^2}R}}$
We know, angular frequency $\omega = 2\pi f'$
$\Rightarrow \mu = \dfrac{g}{{4{\pi ^2}f{'^2}R}}$
Writing the above equation in terms of frequency
$\Rightarrow f{'^2} = \dfrac{g}{{4{\pi ^2}\mu R}}$
$\therefore f' = \dfrac{1}{{2\pi }}\sqrt {\dfrac{g}{{\mu R}}}$

Hence, the minimum frequency of revolution such that a body kept inside of the wall does not slip down is option A.

Note: Centrifugal force is a force that appears to act on a body traveling in a circular route that is directed away from the center around which the body is moving. It is caused by the inertia of the body. The force is also affected by the mass of the object, its distance from the circle's center, and its rotational speed. The force of movement and the speed of the object will be larger if the object has more mass. The force of the movement will be greater if the distance from the circle's center is greater.