Question
Question: A hollow cylinder having infinite length and carrying uniform current per unit length \[\lambda \]al...
A hollow cylinder having infinite length and carrying uniform current per unit length λalong the circumference as shown. Magnetic field inside the cylinder is:
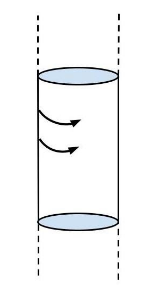
A. 2μ0λ
B. μ0λ
C. 2μ0λ
D. None
Solution
To answer this question, which is based on Biot-Savart's formula, we must first understand it in general. In physics, specifically electromagnetic, the Biot-Savart law describes the magnetic field generated by a continuous electric current. It connects the magnitude, direction, length, and proximity of the electric current to the magnetic field.
Complete step by step answer:
Given that there is current flowing around its circumference.We already know that there will be a magnetic field inside the cylinder is,
4πμ0r′2I′
Where I′ denotes the direction of flow of current and r′ denotes the distance from the centre.
λ is the current length per unit, thus;
λ =2πrI
Therefore, from here we will deduce equation for I
⇒I=λ2πr
At r′ distance from the center, the current inside the cylinder is: I’ = λ2πr’
We've now inserted the value into the equation.
