Question

A hollow cylinder has a charge q coulomb within it. If $\phi$ is the electric flux in units of voltmeter associated with the curved surface B, the flux linked with the plane surface A in units of voltmeter will be
(A) $\dfrac{1}{2}\left( \dfrac{q}{{{\varepsilon }_{0}}}-\phi \right)$
(B) $\dfrac{q}{2{{\varepsilon }_{0}}}$
(C) $\dfrac{\phi }{3}$
(D) $\dfrac{q}{{{\varepsilon }_{0}}}-\phi$

Answer 1

Apply Gauss law to calculate the flux associated with plane surface A. According to Gauss law: The total flux linked with a closed surface is $\dfrac{1}{{{\varepsilon }_{0}}}$ times the charge enclosed by the closed surface. The Gauss Law formula is expressed by :
$\phi =\dfrac{Q}{{{\varepsilon }_{0}}}$
Where Q is total charge within the surface, ${{\varepsilon }_{0}}$ is electrical constant.

Complete step by step solution:
We have given, A hollow cylinder having charge = q coulomb
The electrical flux associated with surface B is ${{\phi }_{B}}=\phi$
The electrical flux associated with surface A and C is ${{\phi }_{A}}$ and ${{\phi }_{C}}$ respectively.

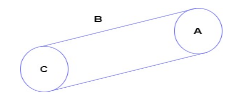
Since surface A and C have the same area of cross section.
So, ${{\phi }_{A}}={{\phi }_{C}}$
Now, apply Gauss Law:
According to which the net electric flux through any closed surface is equal to the net charge inside the surface divided by ${{\varepsilon }_{0}}$ .
${{\phi }_{TOTAL}}={{\phi }_{A}}+{{\phi }_{B}}+{{\phi }_{C}}$ --------(1)
Since, ${{\phi }_{A}}={{\phi }_{C}}$ , ${{\phi }_{B}}=\phi$
From eq. (1) ${{\phi }_{TOTAL}}={{\phi }_{A}}+{{\phi }_{{}}}+{{\phi }_{A}}$
$$ ${{\phi }_{TOTAL}}=2{{\phi }_{A}}+\phi$ --------(2)
By Gauss Law Formula
${{\phi }_{TOTAL}}=\dfrac{q}{{{\varepsilon }_{0}}}$
Using value of eq. (2) in above eq.,
$2{{\phi }_{A}}+\phi =\dfrac{q}{{{\varepsilon }_{0}}}$
$2{{\phi }_{A}}=\dfrac{q}{{{\varepsilon }_{0}}}-\phi$
${{\phi }_{A}}=\dfrac{1}{2}\left( \dfrac{q}{{{\varepsilon }_{0}}}-\phi \right)$ This is the required result.
Hence, option A is correct.

Note:
Gauss Law holds good for any closed surface regardless of its shape and size.
Gauss law is used commonly for symmetric charge distribution.
By Gauss theorem, we can calculate the number of electric lines of force that radiate outwards from one coulomb of positive charge in vacuum.
$\phi =\dfrac{q}{{{\varepsilon }_{0}}},for\text{ }q=1C,\text{ }then\text{ }\phi =\dfrac{1}{8.85\times {{10}^{-12}}}=1.13\times {{10}^{11}}$