Question
Question: A hollow cylinder has a charge \(q\) coulomb within it. If \(\phi \) is the electric flux in units o...
A hollow cylinder has a charge q coulomb within it. If ϕ is the electric flux in units of voltmeter associated with the curved surface Bw, the flux linked with the plane surface A in units of voltmeter will be:
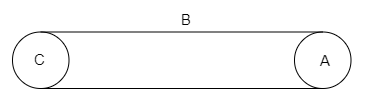
(A) ε0q−ϕ
(B) 21(ε0q−ϕ)
(C) 2ε0q
(D) 3ϕ
Solution
The flux of the wire is given by the equation of the Gauss’s law, and the net flux on the wire is given by the sum of the individual flux of the A, B and C. And by using the given information in the diagram, then the flux in the point A can be determined.
Useful formula
The Gauss’s law gives the relation of flux on the wire, charge on the wire and electric constant of the medium, then
ϕ=ε0q
Where, ϕ is the electric flux of the point, q is the charge in the object and ε0 is the electric constant of the medium.
Complete step by step solution
Given that,
The charge in the hollo cylinder is, q
The electric flux in the hollow cylinder is, ϕ
All the three point are in same hollow cylinder, so the net flux is equal to the sum of the individual flux of the individual points. Then,
ϕ=ϕA+ϕB+ϕC.................(1)
The ends of the hollow cylinder are A and C, so the flux in these two points are same, then
ϕA=ϕC...............(2)
And the net flux is equal to the flux of B, then
ϕ=ϕB....................(3)
Now,
The Gauss’s law gives the relation of flux on the wire, charge on the wire and electric constant of the medium, then
ϕ=ε0q................(4)
Now substituting he equation (1) in the equation (4), then
ϕA+ϕB+ϕC=ε0q...............(5)
Noe substituting the equation (2) and equation (3) in the equation (5), then the above equation is written as,
ϕA+ϕ+ϕA=ε0q
By adding the terms in the above equation, then
2ϕA+ϕ=ε0q
By rearranging the terms in the above equation, then the above equation is written as,
2ϕA=ε0q−ϕ
By keeping the flux of A in one side, then
ϕA=21(ε0q−ϕ)
Hence, the option (B) is the correct answer.
Note: The net flux is equated with the flux of B because in the question it is given that voltmeter shows the flux of the which is connected with the curved wire of the B, so the net flux is equated with the flux of B and the both ends are having the same flux, so flux of A and flux of C are same.
