Question

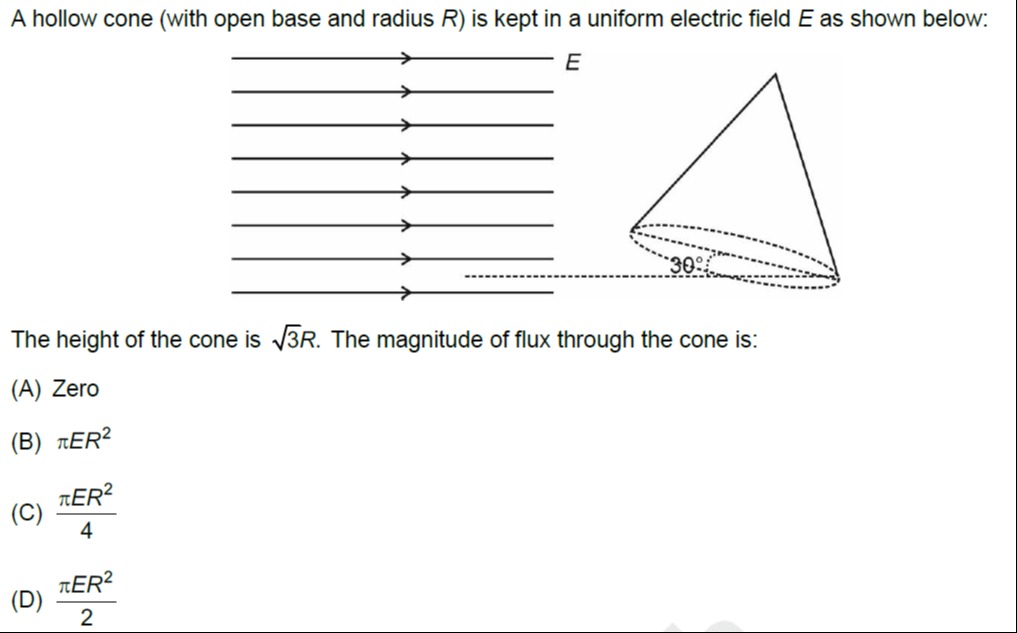
A hollow cone (with open base and radius R) is kept in a uniform electric field E as shown below:

The height of the cone is $\sqrt{3}R$. The magnitude of flux through the cone is:

• A. Zero
• B. $\pi ER^2$
• C. $\frac{\pi ER^2}{4}$
• D. $\frac{\pi ER^2}{2}$

Answer 1

Answer: (B)

$\pi ER^2$

Answer 2

The electric field is uniform. For any closed surface in a uniform electric field, the net electric flux is zero. Consider the given hollow cone with its open base. If we imagine closing this cone with a flat circular base, the combination forms a closed surface. The total flux through this closed surface is zero. This total flux is the sum of the flux through the curved surface of the cone ($\Phi_{curved}$) and the flux through the base ($\Phi_{base}$). Thus, $\Phi_{curved} + \Phi_{base} = 0$, which implies $\Phi_{curved} = -\Phi_{base}$. The magnitude of flux through the cone (curved surface) is therefore equal to the magnitude of flux through its base. The base is a circular disk of radius R, and its area is $\pi R^2$. The uniform electric field E is perpendicular to the base. Hence, the flux through the base is $\Phi_{base} = E \times (\text{Area of base}) = E (\pi R^2)$. Therefore, the magnitude of flux through the cone's curved surface is $\pi E R^2$. The height of the cone is irrelevant for this calculation.