Question

A hollow cone with base radius $acm$ and height $bcm$ is placed on a table. Show that the volume of the largest cylinder that can be hidden underneath is $\dfrac{4}{9}$ times the volume of the cone.

Answer 1

A cylinder is a solid figure, with a circular or oval base or cross section and straight and parallel sides. It is a closed solid figure with two circular bases that are connected by a curved surface. A cone is a solid three-dimensional figure with a flat circular base from which it tapers smoothly to a point known as the vertex.

Complete step by step solution:

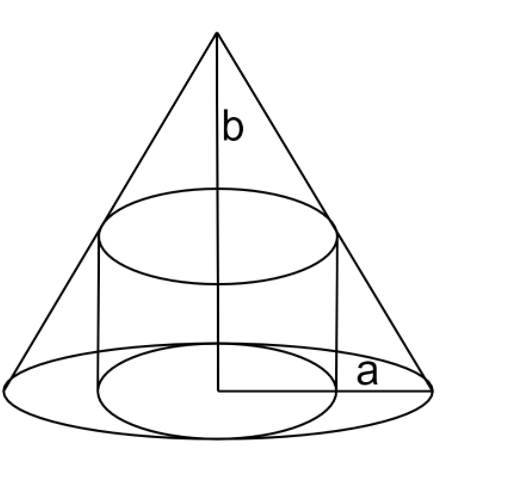
Formulas used in the solution are:
Volume of cylinder $V = \pi {r^2}h$
Where $r$ is the radius of base of the cylinder and $h$ is the height of the cylinder.
Volume of cone $= \dfrac{1}{3}\pi {r^2}h$
Where $r$ is the radius of base of the cone and $h$ is the height of the cone.
Here in this question we are given the following:
The height of cone $= h = b$
The base radius $= r = a$
The base radius of cylinder $= r$
The height of cylinder $= h$
Using similar triangles:
$\dfrac{h}{{a - r}} = \dfrac{b}{a}$
Hence we get ,
$h = \dfrac{b}{a}\left( {a - r} \right) = b - \dfrac{b}{a}r$
Volume of cylinder $V = \pi {r^2}h$
Putting value of $h$ we get ,
$V = \pi {r^2}\left[ {b - \dfrac{b}{a}r} \right]$
$= \pi b{r^2} - \dfrac{{\pi b{r^3}}}{a}$
On differentiating both sides with respect to $r$ we get ,
$\dfrac{{dV}}{{dx}} = \dfrac{{2\pi abr - 3\pi b{r^2}}}{a}$ … $(1)$
Putting $\dfrac{{dV}}{{dx}} = 0$
We get $\pi br(2a - 3r) = 0$
Hence we get $r = \dfrac{{2a}}{3}$
Differentiating $(1)$ with respect to $r$ we get ,
$\dfrac{{{d^2}V}}{{d{r^2}}} = 2\pi b - \dfrac{{6\pi br}}{a}$
Putting value of $r = \dfrac{{2a}}{3}$
$\dfrac{{{d^2}V}}{{d{r^2}}} = 2\pi b - \dfrac{{6\pi b}}{a}\left( {\dfrac{{2a}}{3}} \right)$
$= - 2\pi b$
Therefore $r = \dfrac{{2a}}{3}$ is a maximum point.
So volume is maximum at $r = \dfrac{{2a}}{3}$ .
Therefore we get $h = \dfrac{b}{a}\left( {a - \dfrac{{2a}}{3}} \right) = \dfrac{b}{3}$
Volume of cylinder $= \pi {r^2}h = \pi {\left( {\dfrac{{2a}}{3}} \right)^2}\left( {\dfrac{b}{3}} \right)$
$= \dfrac{4}{9}\left( {\dfrac{1}{3}\pi {a^2}b} \right)$
$= \dfrac{4}{9}$ (volume of cone)
Hence showed.

Note: A cylinder is a solid figure, with a circular or oval base or cross section and straight and parallel sides. It is a closed solid figure with two circular bases that are connected by a curved surface. A cone is a solid three-dimensional figure with a flat circular base from which it tapers smoothly to a point known as the vertex.