Question

A hollow cone floats with its vertical axis upto one-third of the height of a liquid of relative density 0.8 and with its vertex submerged. When another liquid of relative density $\rho$ is filled in it upto one-third of its height, the cone floats up to half its vertical height. The height of cone 0.10 m and radius of cone base is 0.05m. Find the specific gravity $\rho$ is given. (Round it to the closest integer).

Answer 1

In order to solve this question, we need to keep a few things in mind. Firstly, we must know Archimedes' principle, which states that when a body is fully or partially submerged in a liquid, weight of the body is equal to the weight of the liquid displaced. Secondly, we must know the relation of sides in similar triangles.

We must also know that relative density or specific gravity is the density of a material divided by density of water. We also need to know how to find out the volume of a cone.
Finally, we must know that 1 m = 100 cm. Value of acceleration due to gravity $$g=9.8$$$m-{{s}^{-2}}$. Density of water is taken 1$g-c{{m}^{-3}}$. Weight on an object =$mg$, where m is mass.

Formula used:

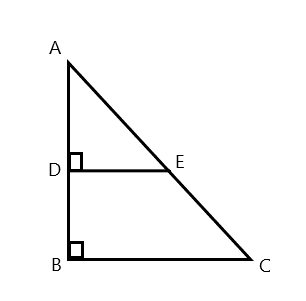
In the above figures triangle ABC and triangle ADE are similar, therefore;
$\dfrac{AD}{AB}=\dfrac{AE}{AC}$
Volume of a right circular cone with height H and radius of base R is:
$V=\dfrac{1}{3}\pi {{R}^{2}}H$

Complete step by step answer:

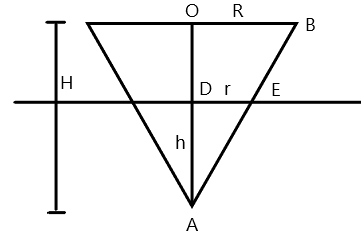
We can see in the above diagram that the cone is submerged in the liquid. The volume of the cone submerged in the liquid is equal to the volume of liquid displaced by the cone.
We are given that $h=\dfrac{1}{3}H$
And triangle ADE and triangle AOB are similar. Therefore,
$\dfrac{r}{R}=\dfrac{h}{H}$, putting $h=\dfrac{1}{3}H$we get,
$r=\dfrac{1}{3}R$
Now, $R=0.05$m or 5 cm and $H=0.10$m or 10 cm.
So, we van get the volume of cone submerged in water,
$=\dfrac{1}{3}\pi {{r}^{2}}h=\dfrac{1}{3}\pi {{\left( \dfrac{5}{3} \right)}^{2}}\dfrac{10}{3}$
$=9.696$ $c{{m}^{3}}$…(1)
Now relative density of liquid $d=\dfrac{{{d}_{liquid}}}{{{d}_{water}}}$
We know the density of water is 1 $g-c{{m}^{-3}}$. Therefore, the density of liquid is equal to the relative density in the cgs system. Hence, ${{d}_{liquid}}=0.8$ $g-c{{m}^{-3}}$.
Now, mass of liquid displaced is equal to volume multiplied by density,
So, $M=d\times volume$
We will get the mass,
$=9.696\times 0.8=7.76$ grams.
We can easily find the weight of water displaced,
$Mass\times g$, where $g=9.8$ $m{{s}^{-2}}$ $=980$ $cm-{{s}^{-2}}$
Hence, we will get value of weight
$980\times 7.76$= 7,604.8 dynes…(2)
According to Archimedes principle the weight of water displaced is equal to the weight of the cone.
Moving forward, the cone is filled with liquid with relative density $\rho$upto one third of its height.
We can find the volume of liquid in the cone which is equal to expression (1). We also know that relative density is equal to density in cgs convention.
Therefore, mass of liquid in cone is equal to volume multiplied by density,
$=9.696\times \rho$grams
From this we can find the gravitational weight of liquid inside the cone,
$9.696\times \rho \times 980=9502.08\rho$dynes…(3)
Now the net weight on the cone is equal to sum of expression (2) and expression (3).
Which is ${{W}_{net}}=7604.8+9502.08\rho$…(4)
Now, the cone is submerged into the liquid with density 0.8 $g-c{{m}^{-3}}$ upto half of its height. There the volume of liquid displaced will be the volume of submerged cones. We know that $h'=\dfrac{H}{2}$, and hence, $r'=\dfrac{R}{2}$ due to the similarity criteria.

Therefore, volume of liquid displaced will be
$=\dfrac{1}{3}\pi {{r}^{2}}h=\dfrac{1}{3}\pi {{\left( \dfrac{R}{2} \right)}^{2}}\dfrac{H}{2}$
$=\dfrac{1}{3}\pi {{\left( \dfrac{5}{2} \right)}^{2}}\dfrac{10}{2}=32.72$ $c{{m}^{3}}$
Now, we can get the mass of liquid displaced

$32.72\times 0.8=26.18$ grams
We can easily find the weight of the liquid displaced,
$26.18\times 980=25656.4$ dynes…(5)
Now, according to Archimedes principle we can equate expression (4) and (5) and get

$\begin{aligned} & 25656.4=7604.8+9502.08\rho \\\ & \Rightarrow 9502.08\rho =18051.6 \\\ & \Rightarrow \rho \approx 2 \\\ \end{aligned}$

Hence, the specific gravity of the liquid is approximately equal to 2.

Note:
Students must remember that the base radius of a cone is different at different heights. They must not confuse it with a cylinder which has the same base radius at any point. All units must be either in the cgs system or SI system.