Question

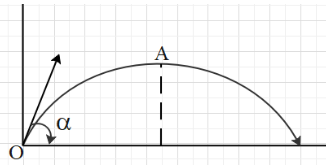
A highest point on the path of a projectile. If the average velocity of the projectile between O and A is $8\widehat{i}+3\widehat{j}$ then $\tan \alpha$ is:

A. $\dfrac{3}{8}$
B. 1
C. $\dfrac{3}{4}$
D. Data is not sufficient

Answer 1

By definition of average velocity we know that average velocity is equal to the net displacement of the body divided by the time taken. Find the displacement and time taken in terms of the initial speed and angle of projection and divide the two to find the average velocity then equate the two vectors and find the required quantity.

Formula used:
$R=\dfrac{{{u}^{2}}\sin 2\alpha }{g}$
$H=\dfrac{{{u}^{2}}{{\sin }^{2}}\alpha }{2g}$
$T=\dfrac{2u\sin \alpha }{g}$
Here, u is the initial velocity of the projectile, $\alpha$ is the angle of projection, g is acceleration due to gravity, R is the horizontal range, H is the maximum height and T is the time of flight.

Complete step by step answer:
From the figure we get that the angle $\alpha$ is the angle at which the projectile is projected. Let the initial speed of the projectile be u. It is given that the average velocity of the projectile when it reaches point A from point O is equal to $8\widehat{i}+3\widehat{j}$. By definition of average velocity we know that average velocity is equal to the net displacement of the body divided by the time taken.Here, the net displacement of the projectile is the line segment joining the points O and A.In this case, the displacement of the projectile when it reaches point A is $d=\dfrac{R}{2}\widehat{i}+H\widehat{j}$, where R us the horizontal range of the projectile and H is the maximum height achieved by it.

We know that $R=\dfrac{{{u}^{2}}\sin 2\alpha }{g}$ and $H=\dfrac{{{u}^{2}}{{\sin }^{2}}\alpha }{2g}$.
Therefore,
$\Rightarrow d=\dfrac{\left( \dfrac{{{u}^{2}}\sin 2\alpha }{g} \right)}{2}\widehat{i}+\dfrac{{{u}^{2}}{{\sin }^{2}}\alpha }{2g}\widehat{j}$
$\Rightarrow d=\dfrac{{{u}^{2}}\sin 2\alpha }{2g}\widehat{i}+\dfrac{{{u}^{2}}{{\sin }^{2}}\alpha }{2g}\widehat{j}$
Now, the time taken to reach point A is equal to $t=\dfrac{T}{2}$, where T is the time of flight of the projectile.
And $T=\dfrac{2u\sin \alpha }{g}$
Then,
$t=\dfrac{2u\sin \alpha }{2g}=\dfrac{u\sin \alpha }{g}$
Therefore, the average velocity of the projectile between points A and O is equal to $\dfrac{d}{t}=\dfrac{\dfrac{{{u}^{2}}\sin 2\alpha }{2g}\widehat{i}+\dfrac{{{u}^{2}}{{\sin }^{2}}\alpha }{2g}\widehat{j}}{\dfrac{u\sin \alpha }{g}}$
$\Rightarrow \dfrac{d}{t}=\dfrac{\dfrac{{{u}^{2}}\sin 2\alpha }{2g}}{\dfrac{u\sin \alpha }{g}}\widehat{i}+\dfrac{\dfrac{{{u}^{2}}{{\sin }^{2}}\alpha }{2g}}{\dfrac{u\sin \alpha }{g}}\widehat{j}$

Here, we can write $\sin 2\alpha =2\sin \alpha \cos \alpha$
Then,
$\Rightarrow \dfrac{d}{t}=\dfrac{\dfrac{2{{u}^{2}}\sin \alpha \cos \alpha }{2g}}{\dfrac{u\sin \alpha }{g}}\widehat{i}+\dfrac{\dfrac{{{u}^{2}}{{\sin }^{2}}\alpha }{2g}}{\dfrac{u\sin \alpha }{g}}\widehat{j}$
$\Rightarrow \dfrac{d}{t}=u\cos \alpha \widehat{i}+\dfrac{u\sin \alpha }{2}\widehat{j}$
But it is given that the average velocity of the projectile between A and O is equal to $8\widehat{i}+3\widehat{j}$.
This means that $u\cos \alpha =8$ …. (i) and $\dfrac{u\sin \alpha }{2}=3$ . …. (ii)
From (i) we get that $u=\dfrac{8}{\cos \alpha }$
Substitute this value in (ii).
$\Rightarrow \dfrac{\dfrac{8}{\cos \alpha }\sin \alpha }{2}=3$
$\Rightarrow 4\tan \alpha =3$
$\therefore\tan \alpha =\dfrac{3}{4}$
Therefore, the initial horizontal velocity of the projectile is ${{u}_{x}}=u\sin \alpha$ and the initial vertical velocity of the projectile is ${{u}_{y}}=u\cos \alpha$.It is given that the point A is the highest point of the projectile. at the highest point the horizontal velocity of the projectile is equal to ${{u}_{x}}=u\sin \alpha$

Hence, the correct option is C.

Note: If you do not understand why we took the time taken as half of the time of flight then know that the motion of the projectile (in absence of air resistance) is symmetric about an vertical axis passing through the highest point (i.e. A). Therefore, the time taken to the reach A is half of the total time to reach ground. If you do not know the formula for H, R and T you also use the suitable kinematic equations in this question.