Question

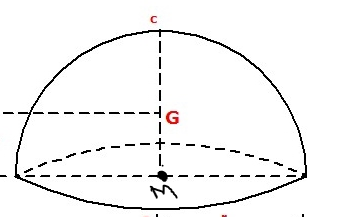
A hemispherical shell of mass $2M$ and radius $6R$ and a point mass $M$ are performing circular motion due to their mutual gravitational interaction. Their positions are shown in figure at any moment of time during motion. If ${{r}_{1}}$ and ${{r}_{2}}$ are radii of circular path of hemispherical shell and point mass respectively and ${{\omega }_{1}}$ and ${{\omega }_{2}}$ are the angular speeds of hemispherical shell and point mass respectively, then choose the correct statement(s).

& A.~~~~~~~~~~\dfrac{{{r}_{1}}}{{{r}_{2}}}=\dfrac{2}{1} \\\ & B.~~~~~~~~~~\dfrac{{{r}_{1}}}{{{r}_{2}}}=\dfrac{1}{2} \\\ & C.~~~~~~~~~~{{\omega }_{1}}=\sqrt{\dfrac{GM}{72{{R}^{2}}}} \\\ & D.~~~~~~~~~~{{\omega }_{2}}=\sqrt{\dfrac{GM}{72{{R}^{2}}}} \\\ \end{aligned}$$

Answer 1

Hint: Here both the bodies will revolve around the centre of mass of the system of hemispherical shell and point mass. In order to calculate radii of circular path of hemispherical shell and point mass, we can calculate their distances from the centre of mass of the system of hemispherical shell and point mass.

Complete Step By Step Solution:
Gravitational forces always occur in an action-reaction pair. The force exerted by one body on another is equal and opposite to the force exerted by the second body on the first. So if we consider both of them a system, net external force on the system is zero. So, the centre of mass of the system is at rest.
When two objects are moving in circular motion due to their mutual gravitational interaction, both of them revolve around the centre of mass of both the objects. This is because their centre of mass is at rest as explained above.
Gravitational field at centre of hemisphere (of mass $2M$ and radius $6R$ ) is given by
$\dfrac{G\left( 2M \right)}{2{{\left( 6R \right)}^{2}}}$
The force exerted by hemispheric shell on point mass or vice-versa is given by
$\dfrac{G\left( 2M \right)\left( M \right)}{2{{\left( 6R \right)}^{2}}}$
The centre of mass of the hemispherical shell is at a distance of half of its radius from the base. So the centre of mass of the hemispherical shell is at $3R$ distance from base (as radius of hemispherical shell is 6R). Now for the centre of mass of the complete system, we will calculate the centre of mass of the point mass and the centre of mass of hemispherical shell.
The distance of the centre of mass of the complete system from the point mass is equal to product of mass of hemispherical shell and distance between hemispherical shell and point mass, divided by the total mass of both. So, mathematically it is
$\dfrac{2M}{2M+M}\left( 3R \right)=2R$
This is also the radius of the circular path of point mass (given in question as ${{r}_{2}}$). So,
${{r}_{2}}=2R$
Similarly the distance of the centre of mass of the complete system from the hemispherical shell is equal to product of point mass and distance between hemispherical shell and point mass, divided by the total mass of both. So, mathematically it is
$\dfrac{M}{2M+M}\left( 3R \right)=R$
This is also the radius of the circular path of the hemispherical shell (given in question as ${{r}_{1}}$). So,
${{r}_{1}}=R$
So, $\dfrac{{{r}_{1}}}{{{r}_{2}}}=\dfrac{1}{2}$
As both the masses are performing circular motion about the centre of mass the gravitational force on them is acting as centripetal force. So for point mass we can write
$\dfrac{G\left( 2M \right)\left( M \right)}{2{{\left( 6R \right)}^{2}}}=M\times {{\omega }_{2}}^{2}\times 2R$,
where ${{\omega }_{2}}$ is angular speeds point mass, $2R$ is its distance from the centre (which is centre of mass of total system)
On solving this we get
${{\omega }_{2}}=\sqrt{\dfrac{GM}{72{{R}^{3}}}}$
Similarly we can solve for ${{\omega }_{1}}$,
$\dfrac{G\left( 2M \right)\left( M \right)}{2{{\left( 6R \right)}^{2}}}=2M\times {{\omega }_{2}}^{2}\times R$
${{\omega }_{1}}=\sqrt{\dfrac{GM}{72{{R}^{3}}}}$

Hence, the correct option is B.

Note: This question can also be solved by dimensional analysis of the options. If we calculate S.I. unit of option C and D, they are not the units of angular speed. So, it is not necessary to calculate the angular speed mathematically for verifying option C and D.