Question

A hemispherical bowl of radius $r$ is set rotating about its axis of symmetry in vertical. A small block kept in the bowl rotates with the bowl without slipping on its surface. If the surface of the bowl is smooth and the angle made by the radius through the block with the vertical is $\theta$. Then, find the angular speed at which the ball is rotating.

& A)\omega =\sqrt{rg\sin \theta } \\\ & B)\omega =\sqrt{\dfrac{g}{r\cos \theta }} \\\ & C)\omega =\sqrt{\dfrac{gr}{\cos \theta }} \\\ & D)\omega =\sqrt{\dfrac{gr}{\tan \theta }} \\\ \end{aligned}$$

Answer 1

The block and bowl are rotating with the same angular velocity. Due to the rotation a centripetal force acts on them. Given that, the radius makes an angle with the vertical axis. Since the block is not slipping on the surface of the block, forces acting on the block are balanced. Here, we can equate the horizontal and vertical components of forces acting on the block. Using the equations for both vertical and horizontal components of forces, we can find the angular velocity of the block.

Formula used:
${{F}_{c}}=m{{\omega }^{2}}{{r}^{'}}$
$N=N\cos \theta +N\sin \theta$
$W=mg$

Complete step by step answer:

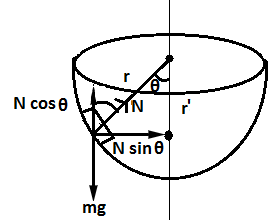
The centripetal force that the rotation exerts on the block, ${{F}_{c}}=m{{\omega }^{2}}{{r}^{'}}$
Where,
$m$ is the mass of the bowl
$\omega$ is the angular velocity
${{r}^{'}}$ is the radius
Since, the block kept in the bowl rotates with the bowl, without slipping on its surface; the forces on the block should balance.
Here, since, the surface of the bowl is smooth; no frictional force is acting on the block. Therefore, the forces that act on the block are normal force $N$ and its weight $mg$ and centripetal force ${{F}_{c}}=m{{\omega }^{2}}{{r}^{'}}$
Horizontal and vertical components normal force are $N\sin \theta$ and $N\cos \theta$.
Vertical forces on the block are equal. Then,

$N\cos \theta =mg$ ---------- 1

Where,

$N$is the normal force acting on the block
$mg$ weight of the block
$\theta$ is the angle made by the radius through the block with the vertical axis of symmetry.
Similarly, the horizontal forces on the block are equal. Then,

$N\sin \theta =m{{\omega }^{2}}{{r}^{'}}$ ---------- 2

Dividing the equation 2 by 1, we get,

$\dfrac{N\sin \theta }{N\cos \theta }=\dfrac{m{{\omega }^{2}}{{r}^{'}}}{mg}$

${{\omega }^{2}}=\dfrac{g\tan \theta }{{{r}^{'}}}$
${{r}^{'}}=r\sin \theta$

Then,

${{\omega }^{2}}=\dfrac{g\tan \theta }{r\sin \theta }=\dfrac{g}{r\cos \theta }$

$\omega =\sqrt{\dfrac{g}{r\cos \theta }}$
The angular speed at which the ball is rotating is $\sqrt{\dfrac{g}{r\cos \theta }}$
Therefore, answer is option B.

Note:
A force that causes a uniform circular motion is known as centripetal force. The direction of a centripetal force is towards the center of curvature. Centripetal force is always perpendicular to the path and pointing to the center of curvature.