Question

A hemispherical bowl of radius $r$ is rotating about its axis of symmetry which is kept vertical. A small block kept in the bowl rotates with the bowl without slipping on its surface. If the surface of the bowl is smooth and the angle made by the radius through the block with the vertical is $\theta$, find the angular speed at which the bowl is rotating.
(A). $\omega =\sqrt{rg\sin \theta }$
(B). $\omega =\sqrt{\dfrac{g}{r\cos \theta }}$
(C). $\omega =\sqrt{\dfrac{gr}{\cos \theta }}$
(D). $\omega =\sqrt{\dfrac{gr}{\tan \theta }}$

Answer 1

Hint: This problem can be solved by equating the magnitude of centripetal force on the block required to continue the rotation with the block to the component of normal force in that direction and equating the weight of the body with the component of the normal force from the bowl that balances it. In equilibrium the sum of the forces is zero on the body.

Formula used:
${{F}_{C}}=m{{\omega }^{2}}R$
where ${{F}_{C}}$ is the centripetal force on a body of mass $m$ rotating on a circle of radius $R$ with angular speed $\omega$.
At equilibrium,
$\sum{\overrightarrow{F}=0}$
where $\overrightarrow{F}$ is a force on the body.

Complete step by step answer:

Firstly let us draw a diagram to understand the problem better.

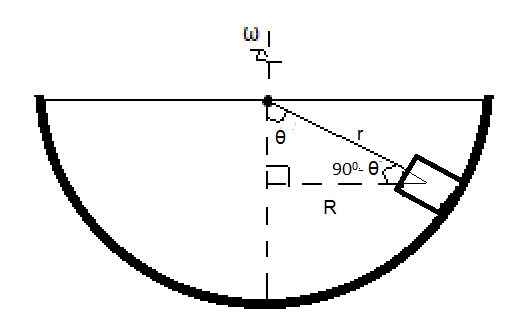
The block essentially rotates in a circle of radius $R$, where
$R=r\sin \theta$ (from geometry of the figure) --(1)
Now, let us draw the free body diagram of the block.

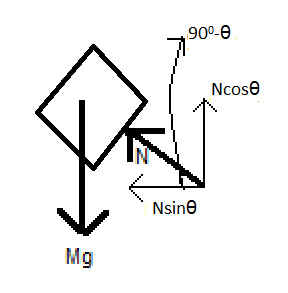
Now,
${{F}_{C}}=m{{\omega }^{2}}R$ --(2)
where ${{F}_{C}}$ is the centripetal force on a body of mass $m$ rotating on a circle of radius $R$ with angular speed $\omega$.
Let the mass of the block be $M$.
The centripetal force is provided by the horizontal component of the normal force from the bowl, that is, $N\sin \theta$. --(3)
The block rotates in a radius of $r$ with the same angular speed as the bowl, that is, $\omega$.
Therefore, from (1), (2) and (3),
$M{{\omega }^{2}}r=N\sin \theta$
$\therefore M{{\omega }^{2}}r\sin \theta =N\sin \theta$
$\therefore M{{\omega }^{2}}r=N$
$\therefore {{\omega }^{2}}=\dfrac{N}{Mr}$ ---(4)
Now, in the vertical direction, the block is in equilibrium. Hence, the vertical component of the normal force cancels out the weight of the block. Hence, from the free body diagram,
$N\cos \theta =Mg$
$\therefore N=\dfrac{Mg}{\cos \theta }$ ---(5)
Putting (5) in (4), we get,
${{\omega }^{2}}=\dfrac{\dfrac{Mg}{\cos \theta }}{Mr}=\dfrac{Mg}{Mr\cos \theta }=\dfrac{g}{R\cos \theta }$
Square rooting both sides, we get,
$\sqrt{{{\omega }^{2}}}=\sqrt{\dfrac{g}{r\cos \theta }}$
$\therefore \omega =\sqrt{\dfrac{g}{r\cos \theta }}$
Hence, the required angular speed of the bowl is $\sqrt{\dfrac{g}{r\cos \theta }}$.
Therefore, the correct option is B) $\omega =\sqrt{\dfrac{g}{r\cos \theta }}$.

Note: For complex problems like these it is always better to draw a proper diagram. Many relations can be devised using geometry in the diagram which makes the problem a lot easier. Since it is easier to visualize and understand a diagram rather than words, the problem becomes very easy upon drawing a diagram.
Students should also check whether the question mentions friction or not. If the bowl had friction, it too would have exerted a force on the ball. This force would have horizontal and vertical components which would have had to be accounted for in the equations. Friction would have provided for extra centripetal force. Hence, for the same problem the bowl could have rotated with greater angular speed if it had friction.