Question
Question: A hemisphere of radius R is just submerged is just sinking in water of density $\rho$. Find the (a)...
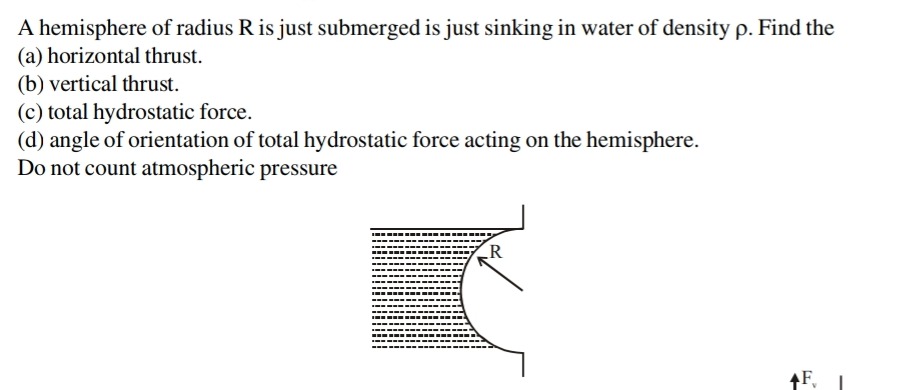
A hemisphere of radius R is just submerged is just sinking in water of density ρ. Find the
(a) horizontal thrust. (b) vertical thrust. (c) total hydrostatic force. (d) angle of orientation of total hydrostatic force acting on the hemisphere. Do not count atmospheric pressure
a) FH=πρgR3, b) FV=32πρgR3, c) Ftotal=3πρgR313, d) θ=arctan(32) with the horizontal
Solution
The problem asks us to determine the horizontal thrust, vertical thrust, total hydrostatic force, and its angle of orientation on a hemisphere of radius R just submerged in water of density ρ. We are to ignore atmospheric pressure. The figure shows the hemisphere embedded in a vertical wall, with its curved surface facing the water, and the water level is at the top of the hemisphere (i.e., at the level of the flat face).
Let's set up a coordinate system. Let the origin be at the center of the flat circular base of the hemisphere. The water surface is at y=0. The hemisphere extends from y=0 to y=−R.
(a) Horizontal Thrust (FH)
The horizontal thrust on a submerged curved surface is equal to the hydrostatic force on the projection of the curved surface onto a vertical plane perpendicular to the direction of the force.
-
Projected Area: The projection of the submerged curved surface of the hemisphere onto a vertical plane (perpendicular to the wall) is a full circle of radius R. The area of this projected circle is Aproj=πR2.
-
Centroid Depth: The centroid of this projected circular area is at its center. Since the water surface is at the top of the hemisphere (which is the top of the projected circle), the depth of the centroid from the free surface is hc=R.
-
Horizontal Force Formula: The horizontal force is given by FH=ρghcAproj. Substituting the values: FH=ρg(R)(πR2) FH=πρgR3 This force acts horizontally, perpendicular to the flat face of the hemisphere, pushing it into the wall.
(b) Vertical Thrust (FV)
The vertical thrust on a submerged curved surface is equal to the weight of the fluid volume vertically above the surface, extending up to the free surface. This is equivalent to the buoyant force for a fully submerged object.
-
Volume of Displaced Fluid: Since the hemisphere is just submerged with its flat face at the water surface, the volume of water displaced by the hemisphere is equal to the volume of the hemisphere itself. The volume of a hemisphere is V=32πR3.
-
Vertical Force Formula: The vertical thrust (buoyant force) is given by FV=ρgV. Substituting the volume: FV=ρg(32πR3) FV=32πρgR3 This force acts vertically upwards.
(c) Total Hydrostatic Force (Ftotal)
The total hydrostatic force is the vector sum of the horizontal and vertical forces. Since FH and FV are perpendicular, the magnitude of the total force is: Ftotal=FH2+FV2 Substituting the calculated values: Ftotal=(πρgR3)2+(32πρgR3)2 Ftotal=(πρgR3)2(1+(32)2) Ftotal=πρgR31+94 Ftotal=πρgR399+4 Ftotal=πρgR3913 Ftotal=3πρgR313
(d) Angle of Orientation of Total Hydrostatic Force (θ)
The angle of orientation of the total hydrostatic force can be found using the components. Let θ be the angle the total force makes with the horizontal. tanθ=FHFV Substituting the values of FV and FH: tanθ=πρgR332πρgR3 tanθ=32 Therefore, the angle of orientation with the horizontal is: θ=arctan(32) The force acts upwards and horizontally away from the wall (if the hemisphere is a cavity) or into the wall (if it's a solid hemisphere as depicted). Given the typical convention, the force is exerted by the fluid on the object.
The direction of FH is horizontal, pushing the hemisphere towards the right (into the wall). The direction of FV is vertical, upwards. So the total force acts at an angle θ=arctan(2/3) above the horizontal, directed towards the wall.
Explanation of the solution:
- Horizontal Thrust (FH): Calculated as the force on the vertical projection of the curved surface. The projection is a circle of radius R. The centroid of this circle is at depth R from the free surface. FH=ρg(depth of centroid)(projected area)=ρgR(πR2)=πρgR3.
- Vertical Thrust (FV): Calculated as the weight of the fluid displaced by the hemisphere (buoyant force). The volume of a hemisphere is 32πR3. FV=ρg(volume displaced)=ρg(32πR3)=32πρgR3.
- Total Hydrostatic Force (Ftotal): The vector sum of the perpendicular horizontal and vertical forces. Ftotal=FH2+FV2=(πρgR3)2+(32πρgR3)2=3πρgR313.
- Angle of Orientation (θ): The angle with the horizontal is given by tanθ=FHFV=πρgR332πρgR3=32. So, θ=arctan(32).
