Question

A hemisphere is uniformly charged positively. The electric field at a point on a diameter away from the center is directed:
(a) Perpendicular to the diameter
(b) parallel to the diameter
(c) At an angle tilted towards the diameter
(d) At an angle tilted away from the diameter

Answer 1

We will use the definition and formula of electric field intensity to find X and Y components of the field. It depends upon the angle present in the formula. As the uniform charge used here is a positive one which is on the surface of the hemisphere so, draw field lines directed outwards from it.

Formula used: $E=E\times S\cos \left( \theta \right)$ where $\theta$ is the angle between electric field lines applied on an object and the normal perpendicular surface to it, E us the magnitude of electric field and S is the area of the surface on which it is applied.

Complete step by step answer:
According to the question we have a hemisphere which is positively charged uniformly. This means that the charge is uniformly distributed all over the surface. Here the surface is taken as a hemisphere.
Electric field intensity: Electric fields are those fields which are applied on a unit positive charge by the action of another charged body. It is always measured by the magnitude of the electric field applied on a certain object with the area of the surface as a consideration. The formula of an electric field is $E=E\times S\cos \left( \theta \right)$.
As per the question, we have a hemisphere with uniform charge distribution all over its surface. This can be seen from the diagram below.

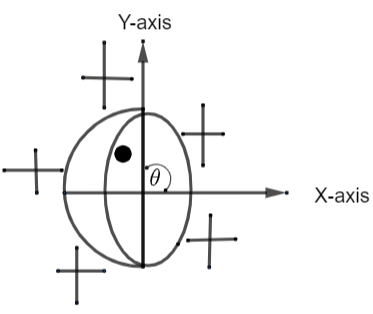
Consider the dot in the figure as a point away from the center but on the diameter of the hemisphere. The field lines along with X-axis is going to be with $\theta ={{0}^{\text{o}}}$ resulting $E=E\times S\cos \left( {{0}^{\text{o}}} \right)$. As $\cos \left( {{0}^{\text{o}}} \right)=1$ so, the field lines along X-axis direction will be $E=E\times S$ and with $\theta ={{90}^{\text{o}}}$ resulting $E=E\times S\cos \left( {{90}^{\text{o}}} \right)$. As $\cos \left( {{90}^{\text{o}}} \right)=0$ so, the field lines along the Y-axis direction will be $E=0$. Clearly the component of the field along with Y-axis cancels out so, this results into the left over electric field which is now present at the X direction.

So, the correct answer is “Option A”.

Note: The most important points to solve such type of question are:
(1) Since, there is a participation of a positively charged particle on the surface on the diameter of hemisphere, which is not at the center, always use electromagnetic field component formula.
(2) If in case the question asks about intensity of electric field on the direction in between X and Y axis, with some angle, then by using $E=E\times S\cos \left( \theta \right)$ we can take this value of intensity.
(3) The electric field intensity is always measured in Volts/meter or Newton/coulomb.
(4) If in case the electric field intensity was asked for a cylinder with the same positive charge uniformly present over it then, as we know that the positive charge always has field lines moving outwards from it then, we will draw the lines for the cylinder and use the formula to find the required intensity.