Question

A helicopter is flying south with a speed of $50\,{\text{km}} \cdot {{\text{h}}^{ - 1}}$. A train is moving at the same speed towards the east. The relative velocity of the helicopter as seen by the passengers in the train will be towards
A. North east
B. South east
C. North west
D. South west

Answer 1

Rewrite the velocities of the helicopter and the train in the vector form. Then calculate the relative velocity of the train with respect to the helicopter. Rearrange the equation for this relative velocity and then calculate the angle between the two directions of the helicopter and the train. Hence, determine the direction of the helicopter seen by the passengers in the train.

Complete step by step answer:
We have given that the helicopter is moving towards south with a speed of $50\,{\text{km}} \cdot {{\text{h}}^{ - 1}}$ and the train is moving towards east with the same speed of $50\,{\text{km}} \cdot {{\text{h}}^{ - 1}}$.
Hence, the velocity of the helicopter can be written as
{\vec v_H} = - 50\,{\text{\hat j}}
The velocity of the train can be written as
{\vec v_T} = 50\,{\text{\hat i}}
The relative velocity ${\vec v_{HT}}$ of the train with respect to the helicopter is given by
${\vec v_{HT}} = {\vec v_H} - {\vec v_T}$
Substitute - 50\,{\text{\hat j}} for ${\vec v_H}$ and 50\,{\text{\hat i}} for ${\vec v_T}$ in the above equation.
{\vec v_{HT}} = - 50\,{\text{\hat j}} - 50\,{\text{\hat i}}
{\vec v_{HT}} = - 50\,{\text{\hat j}} + \left( { - 50\,{\text{\hat i}}} \right)

The diagram representing the directions of the velocity of helicopter, velocity of train and relative velocity of the train with respect to helicopter is as follows:

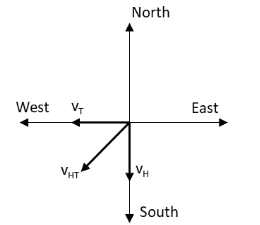
The angle between the relative velocity of the train with respect to helicopter and the velocity of the train and helicopter is given by
$\theta = {\tan ^1}\left( {\dfrac{{{v_H}}}{{{v_T}}}} \right)$
Substitute $- 50\,{\text{km}} \cdot {{\text{h}}^{ - 1}}$ for ${v_H}$ and $- 50\,{\text{km}} \cdot {{\text{h}}^{ - 1}}$ for ${v_T}$ in the above equation.
$\theta = {\tan ^1}\left( {\dfrac{{ - 50\,{\text{km}} \cdot {{\text{h}}^{ - 1}}}}{{ - 50\,{\text{km}} \cdot {{\text{h}}^{ - 1}}}}} \right)$
$\Rightarrow \theta = {\tan ^1}\left( 1 \right)$
$\therefore \theta = 45^\circ$
Therefore, the angle between the velocity of the train with respect to the helicopter with the velocity of the train and helicopter is $45^\circ$.Thus, the direction of the helicopter seen by the passengers in the train is south west.

Hence, the correct option is D.

Note: The students should keep in mind that the direction of the velocity of the train is towards east. But when the values are substituted in the formula for the relative velocity of the train with respect to the helicopter, we can consider the direction of the train towards west. Hence, the direction of the helicopter seen by the passengers in the train is south west.