Question

A helicopter is flying south with a speed of $50\,km{h^{ - 1}}$. A train is moving with the same speed towards east. The relative velocity of the helicopter as seen by the passengers in the train will be $50\sqrt 2 \,km{h^{ - 1}}$ towards
A. northwest
B. southwest
C. northeast
D. southeast

Answer 1

Resolve the components of speed along x-axis and y-axis and apply the parallelogram law of vector addition to find their resultant.

Complete step by step answer:
When two objects A and B are in relative motion, the relative velocity of objectA with respect to the body b be obtained by imposing equal and opposite velocity of B on both A and B, so that B is brought to rest. The resultant of two velocities of A gives the relative velocity of object A with respect to B. As the helicopter is moving along south with a speed of $50\,km{h^{ - 1}}$and train is moving along east with the same speed. This is the same as the case in which a body is moving along the x-axis and the other is moving along the y-axis. There resultant would be given by the the parallelogram law of vector addition = $\sqrt {{{50}^2} + {{50}^2} - 2.50.50\cos 90^\circ } \, = 50\sqrt 2 km{h^{ - 1}}$
As the angle at which helicopter and train are moving is ${90^0}$.

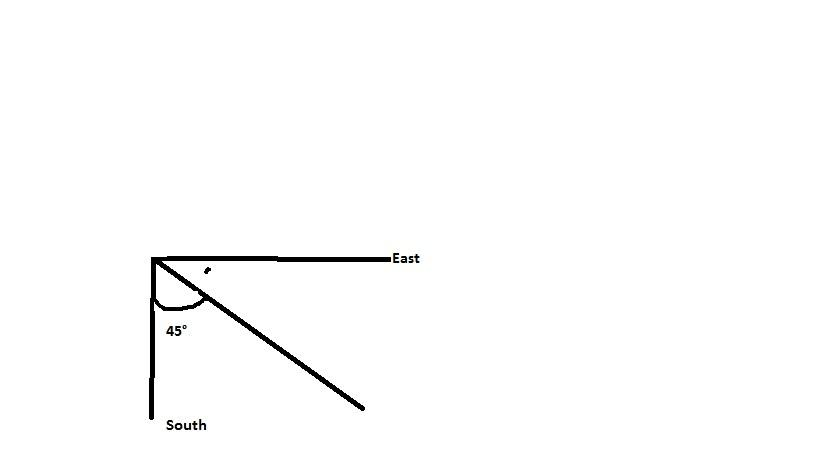
Let the angle of the resultant in the given case be$\theta$. Then
$\tan \theta = \dfrac{{50}}{{50}} = 1 \Rightarrow \theta = 45^\circ$
Hence, the relative velocity of the helicopter as seen by the passengers in the train will be$50\sqrt 2 \,km{h^{ - 1}}$ towards the southeast.

So, the correct answer is “Option D”.

Note:
When a body is moving along x-axis and a body along y-axis. There, resultant velocity will be given by the parallelogram law of vector addition. The parallelogram law of vector addition states that if two bodies are moving along the adjacent sides of a parallelogram, their resultant would be along the diagonal of the parallelogram taken in an order.