Solveeit Logo
Login

Question

Question: A helicopter is flying at 3564m above the ground. If an angle of \({{30}^{\circ }}\) is subtended at...

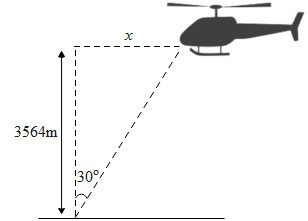
A helicopter is flying at 3564m above the ground. If an angle of 30∘{{30}^{\circ }} is subtended at a ground point by the helicopter position 100s apart, what is the speed of the helicopter?

a) 100ms−1100m{{s}^{-1}}
b)150ms1150m{{s}^{1}}
c)20ms−120m{{s}^{-1}}
d)25ms−125m{{s}^{-1}}

Explanation

Solution

In the above question it is given that the helicopter is flying horizontally at an altitude of 3564m. The helicopter is 100s apart from the vertical line of sight where it is observed from. Hence using the relation between the distance covered, speed and the time taken by the body we will determine the speed of the helicopter.
Formula used:
s=xts=\dfrac{x}{t}

Complete answer:
Let us say there is a body moving in a straight line with speed ‘s’. If the body covers a distance of ‘x’ meters in time ‘t’ the speed of the body is given by,
s=xt....(1)s=\dfrac{x}{t}....(1)
From the above figure we can observe that the helicopter is flying at a height of 3564m from the ground and subtends an angle of 30∘{{30}^{\circ }} when the helicopter is at a distance of ‘x’ m from the vertical line of sight from where it is being observed. Hence using the definition of the tangent of the angle, the distance ‘x’ is equal to,
tan⁡θ=x3564m ∵θ=30∘ tan⁡30∘=x3564m ⇒13=x3564m ∴x=3564m3=2057.67m \begin{aligned} & \tan \theta =\dfrac{x}{3564m} \\\ & \because \theta ={{30}^{\circ }} \\\ & \tan {{30}^{\circ }}=\dfrac{x}{3564m} \\\ & \Rightarrow \dfrac{1}{\sqrt{3}}=\dfrac{x}{3564m} \\\ & \therefore x=\dfrac{3564m}{\sqrt{3}}=2057.67m \\\ \end{aligned}
In the question it is given that the helicopter is 100s away to cover this distance. Hence the speed of the helicopter using equation 1 w get,
s=2057.67m100s ∴s=20.57ms−1≈20ms−1 \begin{aligned} & s=\dfrac{2057.67m}{100s} \\\ & \therefore s=20.57m{{s}^{-1}}\approx 20m{{s}^{-1}} \\\ \end{aligned}

Therefore the correct answer of the above question is option c.

Note:
From the question it is very clear that the helicopter is travelling at constant speed. If the helicopter has some horizontal acceleration, then the above equation for obtaining the speed of the helicopter will be invalid. It is also to be noted that we have approximated the speed of the helicopter as it is expressed in SI units.