Question

A helicopter flies from a city A to B. The line joining A and B is along north-south and its length is 100 km. The speed of the helicopter is kept 100 km/h and wind blows from west to east with a speed of 60 km/h. The time taken by the helicopter is
A. 0.75 h
B. 1.0 h
C. 1.25 h
D. 1.33 h

Answer 1

Use parallelogram law of vector addition considering the wind vector along x-axis and the helicopter velocity along the resultant direction. Find the velocity of the helicopter along the y-axis or AB direction then divide this velocity by distance AB to get the time required.

Formula used:
If A and B are two perpendicular vectors then, by parallelogram law, the magnitude of the resultant is given as:
$C = \sqrt{A^2 + B^2}$

Complete step by step answer:
In the absence of wind, helicopters would have traveled along the AB direction in the north south direction with 100 km/hr speed. But due to the presence of wind along west to east direction, the motion of the helicopter will be affected and the helicopter will have a velocity direction making an angle $\theta$ with the x-axis or (east-west).

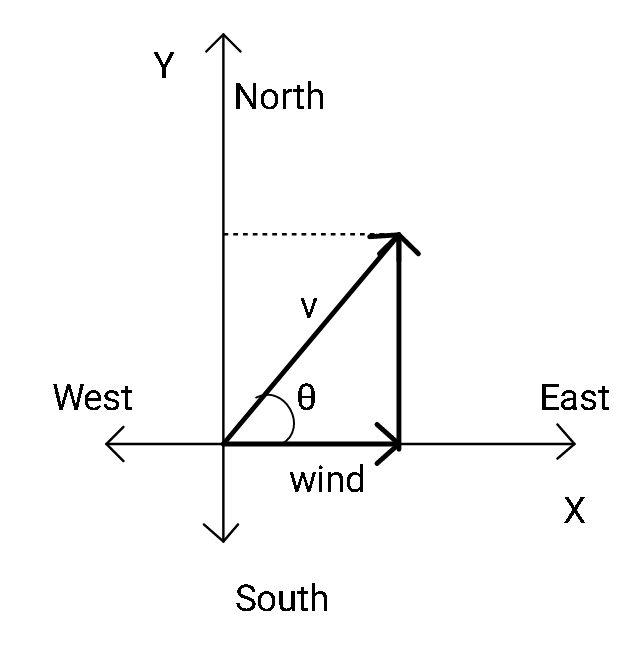
We must find the component of velocity of the helicopter along the y-direction as we assume y-direction to be the direction of AB (or north south direction).
We assume that wind is blowing in positive x-direction (west to east) and we denote wind velocity by a vector. We denote the plane velocity as v and wind velocity as $v_w$ so, from simple Pythagoras theorem; we can see that as v is the hypotenuse of the triangle and we are to find the perpendicular, we write:
$v_{AB} = \sqrt{v^2 - v_w^2}$,
where $v_{AB}$ is the velocity along the AB direction.
Keeping the values we get:
$v_{AB} = \sqrt{(100)^2 - (60)^2} = \sqrt{6400}$ = 80 km/hr .
Thus, the velocity of the helicopter Y direction should be 80 km/hr.

The time required to travel a distance of 100 km with the velocity of 80 km/hr is:
$t = \dfrac{100}{80} = 1.25 hr$.
Therefore, the correct answer is option (C).

So, the correct answer is “Option A”.

Note:
To mark the direction of the helicopter velocity can be a little tricky as the question itself doesn't mention it. It is for us to assume that the resultant motion of the helicopter will be at an angle with the AB direction.