Question

A heavy uniform chain lies on a horizontal table top. If the coefficient of friction between the chain and the table surface is 0.25, then find the maximum % of the length of the chain that can hang over one edge of the table.

A. 20%
B. 25%
C. 35%
D. 15%

Answer 1

Whenever you've got a drag on chains, rods, etc objects having their linear mass densities as a continuing, always use the concept of Mass Gradient. It might make the matter look much easier. We will draw its free-body diagram, showing all the forces working on it, including Normal force and Frictional force. Since the gravity and normal force wipe out one another the body stays in equilibrium along the Y-axis. All you want to check for is the condition for horizontal equilibrium.

Formula used:
${{f}_{\max }}=\mu N$

Complete step by step answer:

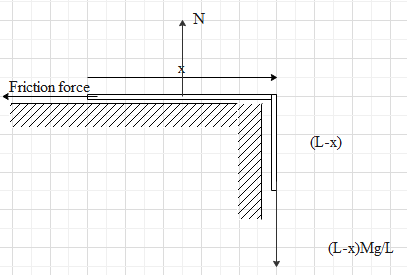
Let x be the length of rope on the table and (L−x) is the length hanging. Let total mass be M.

Therefore mass of hanged part & on table part are
$\dfrac{M}{L}\left( L-x \right)g\text{ and }\dfrac{M}{L}x$

Maximum friction force

${{f}_{\max }}=\mu N=\dfrac{\mu Mgx}{L}$

Weight of the hanging chain,

$W=m'g=\dfrac{M}{L}\left( L-x \right)g=\dfrac{M\left( L-x \right)g}{L}$

For the system to be stable;

$\begin{aligned} & \dfrac{M\left( L-x \right)g}{L}=\dfrac{\mu Mgx}{L} \\\ & \left( L-x \right)=\dfrac{1}{4}x \\\ & x=\dfrac{4}{5}L \\\ & \\\ \end{aligned}$

Therefore the hanging part is $\dfrac{L}{5}$.
Now we will calculate the percentage

$\dfrac{\dfrac{L}{5}}{L}\times 100=20$

The maximum % of the length of the chain that can hang over one edge of the table is 20%.

Note:
For the maximum fraction of length to hang over one edge of the table, we take the limiting load of the chain. The frictional force between the chain lying on the table and the table must balance the tension force because of the chain hanging down for an equilibrium. Be careful when you draw free body diagrams of the extended objects. Always show that gravitational force acts on the Centre of Mass of the body and that frictional force acts along the surfaces in contact. This would help you much when you are also considering the Torques due to different forces.