Question

A heavy small sized sphere is suspended by a string of length $l$. The sphere rotates uniformly in a horizontal circle with the string making an angle $\theta$ with the horizontal. Then the time period of this conical pendulum is
A) $2\pi \sqrt {\dfrac{l}{g}}$
B) $2\pi \sqrt {\dfrac{{l\sin \theta }}{g}}$
C) $2\pi \sqrt {\dfrac{{l\cos \theta }}{g}}$
D) $2\pi \sqrt {\dfrac{l}{{g\cos \theta }}}$

Answer 1

The time required for one complete cycle, i.e. a swing towards the left side and a swing towards the right side, is called the time period. Now, we have to draw the free-body diagram of this system of conical pendulum than all the forces acting on it can be calculated. Thus, calculating the time period.

Complete step by step answer:
Let us first draw the free-body diagram for a better understanding.

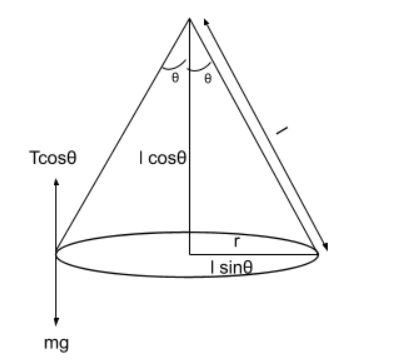
We are given that a conical sphere is suspended by a string of length l. Also, the string is making an angle $\theta$ with the horizontal.
By resolving l along x and y direction and equating we get,
$r = l\sin \theta$
Again, considering the Tension, then two other forces are working, one is the force of gravity and the other is the centrifugal force.
The force of gravity that is working on the conical pendulum can be written as,
${F_g} = mg$,
Where m= mass and g= gravitational constant.
The centripetal force can be written as,
${F_{centri}} = \dfrac{{m{v^2}}}{r}$
Where m= mass, v= velocity, and r= radius of circular motion.
Now, Resolving T along the vertical and horizontal directions, we get,
$T\cos \theta = mg$ ………………..(1)
And
$T\sin \theta = \dfrac{{m{v^2}}}{r}$ …………………(2)
Dividing the above equations, we get
$\Rightarrow \dfrac{{T\cos \theta }}{{T\sin \theta }} = \dfrac{{mg}}{{\dfrac{{m{v^2}}}{r}}} \\\ \Rightarrow \dfrac{{\cos \theta }}{{\sin \theta }} = \dfrac{{rg}}{{{v^2}}} \\\ \Rightarrow \dfrac{1}{{\tan \theta }} = \dfrac{{rg}}{{{v^2}}} \\\$
This can be rewritten as,

$$\Rightarrow v = \sqrt {rg\tan \theta } \\\$$

Again, Time period can be written as,
$T = \dfrac{{2\pi r}}{v}$
Putting the value of $v$ in this equation we get,
$\Rightarrow T = \dfrac{{2\pi r}}{{\sqrt {rg\tan \theta } }} \\\ \Rightarrow T = \dfrac{{2\pi \sqrt r }}{{\sqrt {g\tan \theta } }} \\\ \Rightarrow T = 2\pi \sqrt {\dfrac{r}{{g\tan \theta }}} \\\$
Now, putting the value of $r$ in the equation we get,
$\Rightarrow T = 2\pi \sqrt {\dfrac{{l\sin \theta }}{{g\tan \theta }}} \\\ \Rightarrow T = 2\pi \sqrt {\dfrac{l}{{\dfrac{g}{{\cos \theta }}}}} \\\ \Rightarrow T = 2\pi \sqrt {\dfrac{{l\cos \theta }}{g}} \\\$

Thus, we can see that the right option is (C) $2\pi \sqrt {\dfrac{{l\cos \theta }}{g}}$.

Note:
In this type of problem, it is very necessary to draw a free-body diagram for better understanding. The free-body diagram gives a clear picture of the forces in action and in which direction.