Question

A heavy seesaw (i.e., not massless) is out of balance. A light girl sits on the end that is tilted downward, and a heavy body sits on the other side so that the seesaw now balances. If they both move forward so that they are one-half their original distance from the pivot point (the fulcrum) what will happen to the seesaw?
A. The side the body is sitting on will tilt downward
B. The side the girl is sitting on will once tilt downward
C. Nothing; the seesaw will still be balanced.
D. It is impossible to say without knowing the masses and the distances.

Answer 1

In case of balance, the torque acting on the left hand side of the seesaw balances the torque acting on the right hand side. For the seesaw itself, the force will act at the point of the centre of gravity of the seesaw on the right or left hand side.

Formula Used :
The magnitude of torque acting on a body is given as
$\tau = rF$;
if the body is at a distance r from the pivot and the force is applied at a right angle to the direction of r.

Complete step-by-step answer :
We assume the length of the seesaw to be l and the mass of seesaw on the left side to be more than the mass of seesaw on the right side;
$m_L > m_R$ .

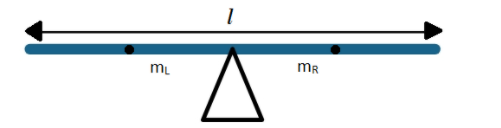
Let the mass of the girl be m and the mass of the heavy body be M.

The center of gravity of the rods of seesaw on left and right sides will be at a distance of l/4 from the centre (or pivot). The girl and body are placed at a distance of l/2 from the pivot initially. Therefore, initially;
$\tau_{left} = \tau_{right}$
$(l/4) m_L g + (l/2)mg = (l/4) m_R g + (l/2)Mg$

Cancelling the common factors on both sides we get:
$\dfrac{m_L - m_R}{2} = M - m$

Now, ask the body and the girl move a distance (l/4) closer to the pivot the net torque will be given as:
$\tau_{net} = \tau_{left} - \tau_{right}$
Where we assume that torque on the left side is bigger, tilting the seesaw to the left side.
$\tau_{net} = \dfrac{l}{4} m_L g +\dfrac{l}{4}mg - \dfrac{l}{4}m_R g - \dfrac{l}{4}Mg$
Or we can write:
$\tau_{net} = lg \left( \dfrac{m_L - m_R + m - M}{4} \right)$ .
Substituting the value of $m_L - m_R$ in terms of m and M, we get:
$\tau_{net} = lg \left( \dfrac{2(M-m) + m - M}{4} \right)$ ;
$\tau_{net} = lg \left( \dfrac{M-m}{4} \right)$
As M is heavy, m is small, our assumption that the left side will tilt is correct as the torque on the left side will dominate.

As the left hand side is where the girl was seated, the correct answer is option (B). The side the girl is sitting on will once again tilt downwards.

Note : Had we assumed that right hand side was tilting or had more torque; we would have found the net talk to be negative. Therefore, in that case we would have found out that the opposite of our assumption is true i.e., left side tilts. Therefore, both the approaches are correct. But one should clearly avoid guesswork at any point in such questions as the chances of getting the right answer decrease in that case.