Question

A heavy ring of mass m is clamped on the periphery of a light circular disc. A small particle having equal mass is damped at the centre of the disc. The system is rotated in such a way that the centre moves in a circle of radius r with a uniform speed $v$ . We conclude that the external force …
A. $\dfrac{{m{v^2}}}{r}$ ,Must be acting on the central particle.
B. $\dfrac{{2m{v^2}}}{r}$ ,Must be acting on the central particle.
C. $\dfrac{{2m{v^2}}}{r}$ ,Must be acting on the system.
D. $\dfrac{{m{v^2}}}{r}$, Must be acting on the ring.

Answer 1

To find out the force on the system of particles , first treat the bodies of the system as a whole system then apply the formula on the centre of mass of the system. Here total of mass 2m is moving with velocity ( v ) so the centrifugal force on the system of particle is ${F_C} = \dfrac{{{m_{system}}{{(velocity)}^2}}}{{radius\;ofc.o.m}}$.

Complete Step by step solution :
The situation is shown here

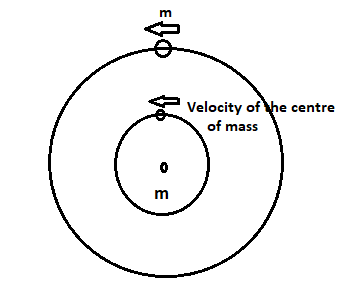
${F_C}$

Let us consider the heavy ring of mass m is clamped on the periphery of a light circular disc and a small particle having equal mass is damped at the centre of the disc as a system. Then the centre of mass of the system has a total of mass 2m.

Now, it is given that the centre of mass moves with velocity v in a circle , so due to this circular motion of the centre of mass there will be a centrifugal force .
$\Rightarrow {F_C} = \dfrac{{{m_{system}}{{(velocity)}^2}}}{{radius\;ofc.o.m}}$
Putting the values ${m_{system}} = 2m$; $velocity = v$; $radius\;ofc.o.m = r$
$\Rightarrow {F_C} = \dfrac{{2m{v^2}}}{r}$
Since, $\dfrac{{2m{v^2}}}{r}$ ,Must be acting on the system as a centrifugal force ,

Hence option ( C ) is the correct answer.

Note:
When a body moves in a circular motion there acts a force due to which the particle still continues its path in a circle and this force is constant in nature if the velocity of the body is constant and called as centripetal force.
The value of the centripetal force is
${F_{centripetal}} = \dfrac{{{m_{body}}{{(velocity)}^2}}}{{radius\;of circle}}$.