Question

A heavy chain of length 1m and weight 20kg hangs vertically with one end attached to a peg and carries a block of mass 10kg at the other end. Find the work done in winding 50cm of chain around the peg.
A. 85J
B. 100J
C. 120J
D. 125J

Answer 1

We will be using the work energy theorem and conservation of energy formula to solve this problem. According to the work energy theorem, net work done is equal to the difference of the final and initial kinetic energies. That is: ${{W}_{net}}=K.{{E}_{final}}-K.{{E}_{initial}}=\Delta K$. According to the conservation of energy formula, the sum of change in kinetic and potential energies is zero. That is: $\Delta E=\Delta U+\Delta K=0$. Hence; ${{W}_{net}}=-\Delta U$. The potential energy (U) in this case is given by: U=mgh.

Let’s start by making a diagram of the problem.

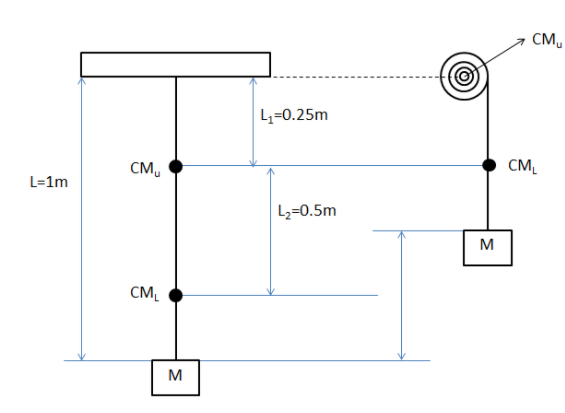
The length of the chain of weighing 20kg is 1m. We will break the whole mass of the heavy chain into two equal components which are centre of mass of equal mass 10kg. These centre of masses are at equal distances from the mid length of the chain and from the top and bottom of the chain. We will call the centre of mass of the upper half of the chain as$\left( C.{{M}_{U}} \right)$and the centre of mass of the lower half of the chain as$\left( C.{{M}_{L}} \right)$. The length of the chain from the peg till $C.{{M}_{U}}$is ${{L}_{1}}=0.25m$. The distance between the two centres of masses is ${{L}_{2}}=0.5m$. The block of mass (M), where M=10kg is attached to the bottom of the chain.
Then, a certain amount of work (W) is done to wind up 50cm, that is 0.5m of the chain on the peg from which it is hanging. Hence, this causes the centre of mass of the upper part of the chain$\left( C.{{M}_{U}} \right)$ to get transferred to the centre of the peg on which it is winded and the centre of mass of the lower part of the chain$\left( C.{{M}_{L}} \right)$ and the block is displaced upwards by 0.5m.
Since, no change in kinetic energy is observed, hence the work energy theorem, which states that net work done is equal to the difference of the final and initial kinetic energies. That is: ${{W}_{net}}=K.{{E}_{final}}-K.{{E}_{initial}}=\Delta K$. And according to the conservation of energy formula, the sum of change in kinetic and potential energies is zero. That is: $\Delta E=\Delta U+\Delta K=0$. Hence; ${{W}_{net}}=-\Delta U$. That is the change in the potential energy of the system will give us the work done. We know that the potential energy formula is: U=mgh.
$\because \Delta U=mg({{h}_{f}}-{{h}_{i}})\Rightarrow \Delta U=\left( C.{{M}_{U}} \right)g\left( 0-0.25 \right)+\left( C.{{M}_{L}} \right)g\left( 0.25-0.75 \right)+Mg(0.5-1)$.
That is; $\Delta U=10g\left( -0.25 \right)+10g\left( -0.5 \right)+10g(-0.5)\Rightarrow \Delta U=-10g(1.25)$.
Hence, the net work done is: {{W}_{net}}=-\Delta U\Rightarrow {{W}_{net}}=-\left\\{ -10g\left( 1.25 \right) \right\\}\Rightarrow {{W}_{net}}=12.5g.
If we consider,$\left( g=10m{{s}^{-2}} \right)$, then the net work done becomes: ${{W}_{net}}=12.5(10)\Rightarrow {{W}_{net}}=125J$, given by Option D.

Note: One may be tempted to attempt to find the change in the potential energy$\left( \Delta U \right)$, by finding the potential energy of the system initially and then finding the potential energy at the final stage. However, this isn’t possible, since we aren’t given the value of the height of the masses from the ground but only the length of the chain. Hence, we need to use the change in the length to find the difference in the potential energy, since the height from the ground with respect to the masses will be a constant, that will be removed when we consider the change in the lengths, as used in solving the problem above.