Question

A heavy box is dragged along a horizontal floor. To do so, a person A pushes it at an angle ${30^ \circ }$ from the horizontal and requires a minimum force ${F_A}$, while person B pulls the box at an angle ${60^ \circ }$ from the horizontal and needs minimum force ${F_B}$. If the coefficient between the box and the floor is $\dfrac{{\sqrt 3 }}{5}$, find the ratio $\dfrac{{{F_A}}}{{{F_B}}}$.
(A) $\sqrt 3$
(B) $\dfrac{5}{{\sqrt 3 }}$
(C) $\sqrt {\dfrac{3}{2}}$
(D) $\dfrac{2}{{\sqrt 3 }}$

Answer 1

Hint
To solve this question, we need to resolve the axial force applied on the block into perpendicular components in both the cases. The contact forces, namely the normal reaction and hence the frictional force will be obtained in terms of these components, when the equilibrium of the block is considered.
Formula Used: The formula used in solving this question is given by
$\Rightarrow F = \mu N$, where $f$ is the value of the frictional force acting between a given pair of surfaces having the value of coefficient of friction as $\mu$ and the normal reaction between the surfaces is $N$.

Complete step by step answer
In this question, we have two cases, the first is the case of pushing and the second is the case of pulling.
Case I:
The free body of the block is shown in the figure below.

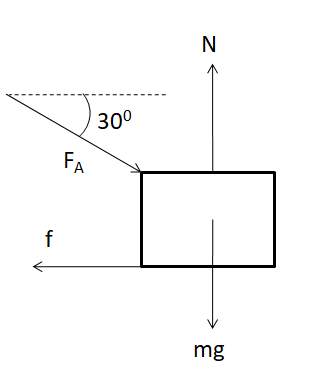
From the equilibrium of the block in the vertical direction
$\Rightarrow N - mg - {F_A}\sin {30^ \circ } = 0$
$\Rightarrow N = mg + {F_A}\sin {30^ \circ }$
So we get the normal reaction from the floor as
$\Rightarrow N = mg + \dfrac{{{F_A}}}{2}$ ………………..(i)
Since the force applied is minimum, so it is just sufficient to overcome the maximum limit of the frictional force. So we have
$\Rightarrow {F_A}\cos {30^ \circ } = f$
$\Rightarrow \dfrac{{\sqrt 3 }}{2}{F_A} = \mu N$
From (i) we have
$\Rightarrow \dfrac{{\sqrt 3 }}{2}{F_A} = \mu \left( {mg + \dfrac{{{F_A}}}{2}} \right)$
According to the question $\mu = \dfrac{{\sqrt 3 }}{5}$
Substituting this above
$\Rightarrow \dfrac{{\sqrt 3 }}{2}{F_A} = \dfrac{{\sqrt 3 }}{5}\left( {mg + \dfrac{{{F_A}}}{2}} \right)$
Cancelling $\sqrt 3$ from both the sides
$\Rightarrow \dfrac{{{F_A}}}{2} = \dfrac{1}{5}\left( {mg + \dfrac{{{F_A}}}{2}} \right)$
$\Rightarrow \dfrac{{{F_A}}}{2}\left( {1 - \dfrac{1}{5}} \right) = \dfrac{{mg}}{5}$
On solving we get
$\Rightarrow {F_A} = \dfrac{{mg}}{2}$ ………………..(ii)
Case II:
The free body of the block for this case is shown in the figure below.

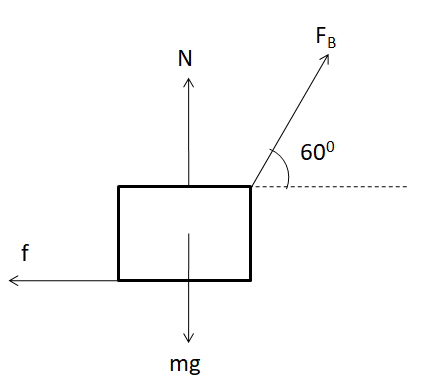
From the equilibrium of the block in the vertical direction
$\Rightarrow N - mg + {F_B}\sin {60^ \circ } = 0$
$\Rightarrow N = mg - {F_B}\sin {60^ \circ }$
So we get the normal reaction from the floor as
$\Rightarrow N = mg - \dfrac{{\sqrt 3 }}{2}{F_B}$ ………………..(iii)
Since the force applied is minimum, so it is just sufficient to overcome the maximum limit of the frictional force. So we have
$\Rightarrow {F_B}\cos {60^ \circ } = f$
$\Rightarrow \dfrac{1}{2}{F_B} = \mu N$
From (iii) we have
$\Rightarrow \dfrac{1}{2}{F_B} = \mu \left( {mg - \dfrac{{\sqrt 3 }}{2}{F_B}} \right)$
According to the question $\mu = \dfrac{{\sqrt 3 }}{5}$
Substituting this above, we get
$\Rightarrow \dfrac{{{F_B}}}{2} = \dfrac{{\sqrt 3 }}{5}\left( {mg - \dfrac{{\sqrt 3 }}{2}{F_B}} \right)$
$\Rightarrow \dfrac{{{F_B}}}{2} = \dfrac{{\sqrt 3 }}{5}mg - \dfrac{3}{{10}}{F_B}$
On rearranging we have
$\Rightarrow \dfrac{{{F_B}}}{2} + \dfrac{{3{F_B}}}{{10}} = \dfrac{{\sqrt 3 }}{5}mg$
Taking the LCM
$\Rightarrow \dfrac{{8{F_B}}}{{10}} = \dfrac{{\sqrt 3 }}{5}mg$
On solving we get
$\Rightarrow {F_B} = \dfrac{{\sqrt 3 }}{4}mg$ ………………..(iv)
Finally, dividing (ii) by (iv), we get
$\Rightarrow \dfrac{{{F_A}}}{{{F_B}}} = \dfrac{{\dfrac{{mg}}{2}}}{{\dfrac{{\sqrt 3 }}{4}mg}}$
$\Rightarrow \dfrac{{{F_A}}}{{{F_B}}} = \dfrac{2}{{\sqrt 3 }}$
Hence, the correct answer is option D.

Note
Do not forget to evaluate the normal reaction separately for each of the two cases given in the question. It is a common misconception that the normal reaction offered by a horizontal surface is always equal to the weight of the object.