Question

A heavy block of mass $m$ is supported by a cord $C$ from the ceiling, and another cord $D$ is attached to the bottom of the block. If a sudden jerk is given to $D$, then:

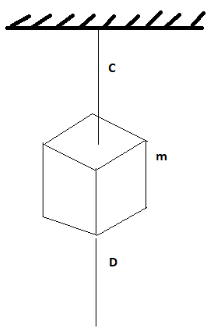
(A) Cord $C$ breaks
(B) Cord $D$ breaks
(C) Cord $C$ and $D$ both break
(D) None of the cord breaks

Answer 1

First of all, we will find out that the weight of the block is acting downward, while the tension is acting upward in the cord $C$. Any cord will withstand the balancing of forces unless it exceeds the magnitude of balancing force.

Complete step by step answer:
In the given question, we are supplied with the following data:
-There is a heavy block whose mass is $m$ .It is supported by a cord $C$ from the ceiling.
However, a cord $D$ is also attached to the block to the bottom.Then a sudden jerk is given at the point $D$ and we are asked to find out what will happen to the block and the cords present with it.
-To begin with, we will analyse the situation of the block and the cords. We know that the weight of a body always acts downwards. So, in this case too, the weight of the block will act downward and since the cord $C$ is holding the block, the whole weight of the block is balanced by the tension force, which is acting in the upward direction. All the weight force of the block is transferred to the upper cord. In such a case, the lower cord which is named as $D$ suffers no tension force, however it is just attached to the block to the bottom. No force is acting on it.
-In such a case, if the lower cord is given a jerk, then the whole equilibrium will be disturbed, as the upper cord is balancing the block. In such a case, the jerk adds more force on the block, which exceeds the capacity of the upper cord $C$. Eventually, the cord $C$ breaks due to high tension in it. However, the cord $D$ has nothing to do with it. It does not break.

Hence,the correct option is A.

Note: Most of the students tend to make mistakes that the cord $D$ breaks, however this is not correct, as the whole weight of the block is acting on the cord $C$. Unable to bear the high stress the cord $C$ breaks off. Weight always acts downward while the tension force acts upwards.