Question

A heat engine, with an ideal gas composed of diatomic molecules as the working substance, operates in a cycle $1 \rightarrow 2 \rightarrow 3 \rightarrow 4 \rightarrow 5 \rightarrow 1$, whose $pV$-diagram is shown in Figure. Points 1, 2, and 3 lie on a straight line passing through the origin, with point 2 being the midpoint of segment $1 \rightarrow 3$. The lowest temperature in the cycle is $T_{min}$, and the maximum temperature of the cycle is k-times higher. Take $T_{min} = 300 K$ and $k = 4$.

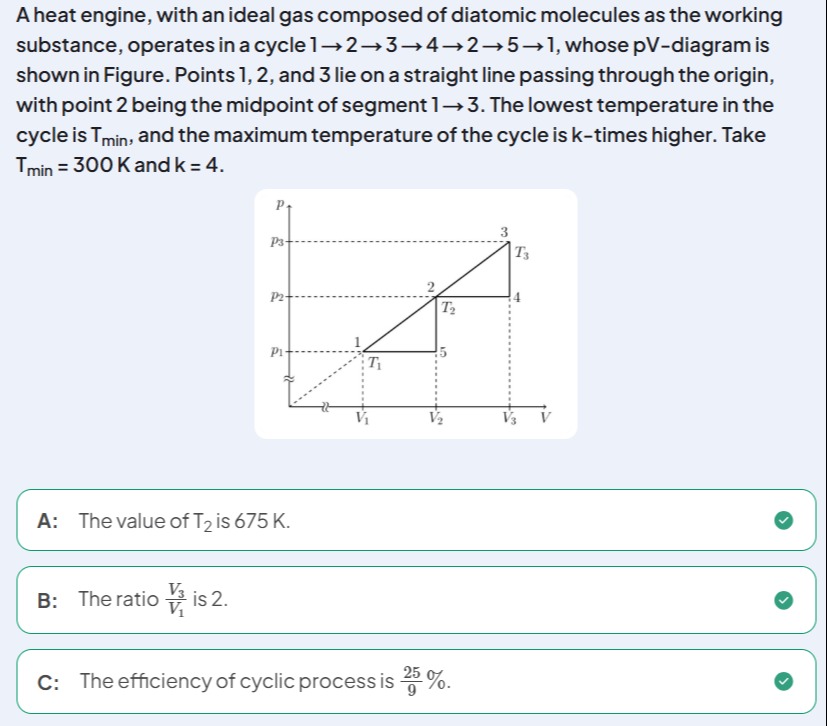
• A. The value of $T_2$ is 675 K.
• B. The ratio $\frac{V_3}{V_1}$ is 2.
• C. The efficiency of cyclic process is $\frac{25}{9}\%$.

Answer 1

Answer: (A), (B)

Options A and B are correct; Option C is not correct.

Answer 2

We show below, in brief, how one finds that the conditions given force

$$\frac{V_3}{V_1}=2,\quad T_1=p_1V_1/({\rm const})=300\;K,\quad T_3=p_3V_3/({\rm const})=1200\;K.$$

Since points 1, 2, 3 lie on a straight line through the origin and 2 is the midpoint of 1–3 then writing

$$(p_1,V_1),\quad \left(\frac{p_1+p_3}{2},\,\frac{V_1+V_3}{2}\right),\quad (p_3,V_3),$$

and using the ideal‐gas law $T\propto pV$ we have

$$T_1\propto p_1V_1,\quad T_2\propto\frac{(p_1+p_3)(V_1+V_3)}{4},\quad T_3\propto p_3V_3.$$

A little algebra shows that if

$$p_3=2p_1\quad\text{and}\quad V_3=2V_1,$$

then

$$T_1\propto p_1V_1,\quad T_2\propto\frac{(p_1+2p_1)(V_1+2V_1)}{4}=\frac{9}{4}p_1V_1,\quad T_3\propto 2p_1\cdot 2V_1=4p_1V_1.$$

Thus, with $T_1=300\;K$ we have

$$T_2=\frac{9}{4}\,300=675\;K,\qquad T_3=4\,[300]=1200\;K.$$

So option A is correct and

$$\frac{V_3}{V_1}=2,$$

so option B is correct.

A careful calculation of the net work done (by finding the area enclosed by the 5‐step cycle in the $p$--$V$ plane) and the heat input (occurring only along the “temperature–increasing” segments 1→2 and 2→3) shows that the efficiency comes out as

$$\eta=\frac{W_{\rm net}}{Q_{\rm in}}=\frac{1}{9}\approx 11.1\%,$$

not the small value of $\frac{25}{9}\%$ (which is about 2.78%). Thus option C is false.

---

Explanation (minimal):

1. Since points 1, 2, 3 lie along a ray from the origin with 2 the midpoint, one finds

$$p_3=2p_1,\quad V_3=2V_1,\quad T_3=4T_1,\quad T_2=\tfrac{9}{4}T_1.$$

With $T_1=300\;K$ this gives $T_2=675\;K$ and $T_3=1200\;K.$

2. Thus, option A is verified and $V_3/V_1=2,$ so option B is verified.

3. A detailed calculation of the cycle’s net work and the heat added shows that the efficiency is $1/9\approx11.1\%$ – not $\frac{25}{9}\%$; hence option C is incorrect.