Question
Question: A handclap on stage in an amphitheatre sends out sound waves that scatter from terraces of width \[w...
A handclap on stage in an amphitheatre sends out sound waves that scatter from terraces of width w=0.75 m. The sound returns to the stage as a periodic series of pulses, one from each terrace; the parade of pulses sounds like a played note. (a) Assuming that all the rays in the figure are horizontal, find the frequency at which the pulses return (that is, the frequency of the perceived note). (b) If the width w of the terraces were smaller, would the frequency be higher or lower?
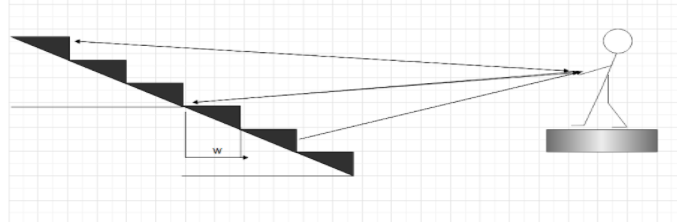
Solution
Since the returning pulse rays are assumed to be horizontal, the frequency could be calculated by using the inverse relation with time period. So first we have to find the time period using the simple relation with distance and speed of sound.
Complete answer:
We know that the speed of sound in air,
v=343 ms−1
(a) Since the amphitheatre is made up of terraces of width,
w=0.75 m
There is a difference in the amount of time taken by each pulse ray. That is why, the parade of pulses sounds like a played note and this time lag is clearly heard by the person who clapped.
This time period can be calculated by the formula,
T=v2w
Substituting the values, we get,
