Question

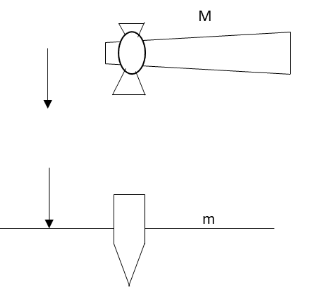
A hammer of mass $M$ falls from a height $h$ repeatedly to drive a pile of mass $m$ into the ground. The hammer makes the pile penetrate in the ground to a distance $d$ in a single blow. Opposition to penetration is given by:

A. $\dfrac{{{m^2}gh}}{{M + md}}$
B. $\dfrac{{{m^2}gh}}{{\left( {M + m} \right)d}} + \left( {M + m} \right)g$
C. $\dfrac{{{M^2}gh}}{{M + md}}$
D. $\dfrac{{{m^2}gh}}{{\left( {m + M} \right)d}} + \left( {M + m} \right)g$

Answer 1

First use the kinematic equation for final velocity in terms of displacement to calculate the final velocity of the hammer when it falls on the mass. Then determine the velocity of the hammer-mass system after it starts penetrating in the ground using the law of conservation of linear momentum. Then use the work-energy theorem and calculate the opposition force for the penetration.

Formulae used:
The kinematic equation for the final velocity of an object in terms of its displacement is
${v^2} = {u^2} + 2as$ …… (1)
Here, $v$ is final velocity of the object, $u$ is initial velocity of the object, $a$ is acceleration of the object and $s$ is displacement of the object.
The kinetic energy $K$ of an object is
$K = \dfrac{1}{2}m{v^2}$ …… (2)
Here, $m$ is the mass of the object and $v$ is the velocity of the object.
The potential energy $U$ of an object is
$U = mgh$ …… (3)
Here, $m$ is the mass of the object, $g$ is acceleration due to gravity and $h$ is the height of the object from the ground.
The work done $W$ is given by
$W = Fd$ …… (4)
Here, $F$ is the force acting on the object and $d$ is the displacement of the object.

Complete step by step answer:
We have given that a hammer of mass $M$ falls on a mass $m$ and this mass penetrates in the ground up to a distance $d$.We have asked to determine the opposition force for penetration of mass into the ground.Let us first calculate the velocity with which the hammer falls on the mass.The initial velocity of the hammer at height $h$ from the mass is zero.Rewrite equation (1) for the vertical motion of the hammer.
$v_y^2 = u_y^2 + 2gh$
$\Rightarrow v_y^2 = {\left( {0\,{\text{m/s}}} \right)^2} + 2gh$
$\Rightarrow {v_y} = \sqrt {2gh}$
This is the expression for velocity with which the hammer falls on mass.

Let us now calculate the combined velocity of the hammer and mass with which they penetrate into the ground.According to the law of conservation of linear momentum, the linear momentum of the hammer and mass system before the hammer falls on the mass is equal to the linear momentum of the hammer-mass system after the mass starts penetrating into ground.
$M\sqrt {2gh} = \left( {M + m} \right)v$
$\Rightarrow v = \dfrac{{M\sqrt {2gh} }}{{\left( {M + m} \right)}}$
This is the expression for velocity of the hammer-mass system while penetrating in the ground.

Let us now use the work-energy theorem to calculate the opposition force.The work done $W$ by the bet force $F$ on the system is equal to change in kinetic energy of the hammer-mass system.
$W = {K_f} - {K_i}$
The initial kinetic energy of the hammer-mass system is zero.The net force on the hammer-mass system is due to the opposition force $F$ and weight of the system $\left( {M + m} \right)g$.
${F_{net}} = F - \left( {M + m} \right)g$
Substitute ${F_{net}}d$ for $W$, $\dfrac{1}{2}\left( {M + m} \right){v^2}$ for ${K_f}$ and $0\,{\text{J}}$ for ${K_i}$ in the above equation.
${F_{net}}d = \dfrac{1}{2}\left( {M + m} \right){v^2} - \left( {0\,{\text{J}}} \right)$
$\Rightarrow {F_{net}}d = \dfrac{1}{2}\left( {M + m} \right){v^2}$

Substitute $F - \left( {M + m} \right)g$ for ${F_{net}}$ and $\dfrac{{M\sqrt {2gh} }}{{\left( {M + m} \right)}}$ for $v$ in the above equation.
$\Rightarrow \left[ {F - \left( {M + m} \right)g} \right]d = \dfrac{1}{2}\left( {M + m} \right){\left( {\dfrac{{M\sqrt {2gh} }}{{\left( {M + m} \right)}}} \right)^2}$
$\Rightarrow Fd = \dfrac{1}{2}\left( {M + m} \right)\left( {\dfrac{{{M^2}\left( {2gh} \right)}}{{{{\left( {M + m} \right)}^2}}}} \right) + \left( {M + m} \right)gd$
$\therefore F = \dfrac{{{M^2}gh}}{{\left( {M + m} \right)d}} + \left( {M + m} \right)g$
Therefore, the opposition to penetration is $\dfrac{{{M^2}gh}}{{\left( {M + m} \right)d}} + \left( {M + m} \right)g$.

Hence, the correct option is B.

Note: The students should not forget to determine the net force while using the formula for the work done. If we consider only the opposition force while determining the work done then the final expression for the opposition force will not be correct. The students should not forget to consider the weight of the hammer-mass system.