Question

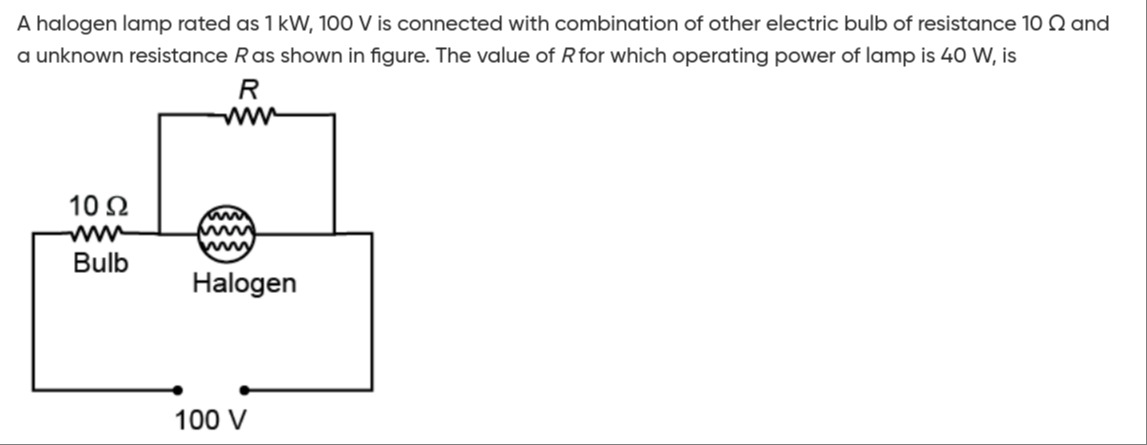
A halogen lamp rated as 1 kW, 100 V is connected with combination of other electric bulb of resistance 10 $\Omega$ and a unknown resistance $R$ as shown in figure. The value of $R$ for which operating power of lamp is 40 W, is

Answer 1

10/3 $\Omega$

Answer 2

The problem requires us to find the value of an unknown resistance $R$ in a given circuit configuration.

1. Calculate the resistance of the halogen lamp ($R_{halogen}$): The halogen lamp is rated at $P_{rated} = 1 \text{ kW} = 1000 \text{ W}$ and $V_{rated} = 100 \text{ V}$. The resistance of the lamp can be calculated using the formula $P = \frac{V^2}{R}$: $R_{halogen} = \frac{V_{rated}^2}{P_{rated}} = \frac{(100 \text{ V})^2}{1000 \text{ W}} = \frac{10000 \text{ V}^2}{1000 \text{ W}} = 10 \text{ } \Omega$.

2. Calculate the operating voltage across the halogen lamp ($V_{halogen}$): The operating power of the lamp is given as $P_{operating} = 40 \text{ W}$. Using the lamp's resistance, we can find the voltage across it at this operating power: $P_{operating} = \frac{V_{halogen}^2}{R_{halogen}}$ $40 \text{ W} = \frac{V_{halogen}^2}{10 \text{ } \Omega}$ $V_{halogen}^2 = 40 \text{ W} \times 10 \text{ } \Omega = 400 \text{ V}^2$ $V_{halogen} = \sqrt{400} \text{ V} = 20 \text{ V}$.

3. Determine the voltage across the unknown resistance R ($V_R$): From the circuit diagram, the halogen lamp and the unknown resistance $R$ are connected in parallel. In a parallel combination, the voltage across each component is the same. Therefore, $V_R = V_{halogen} = 20 \text{ V}$.

4. Determine the voltage across the 10 $\Omega$ bulb ($V_{bulb}$): The entire circuit is connected to a $V_{total} = 100 \text{ V}$ source. The 10 $\Omega$ bulb is in series with the parallel combination of the halogen lamp and resistance $R$. The total voltage is divided between the series bulb and the parallel combination: $V_{total} = V_{bulb} + V_{halogen}$ $100 \text{ V} = V_{bulb} + 20 \text{ V}$ $V_{bulb} = 100 \text{ V} - 20 \text{ V} = 80 \text{ V}$.

5. Calculate the current through the 10 $\Omega$ bulb ($I_{bulb}$): The resistance of this bulb is $R_{bulb} = 10 \text{ } \Omega$. Using Ohm's law: $I_{bulb} = \frac{V_{bulb}}{R_{bulb}} = \frac{80 \text{ V}}{10 \text{ } \Omega} = 8 \text{ A}$.

6. Calculate the current through the halogen lamp ($I_{halogen}$): $I_{halogen} = \frac{V_{halogen}}{R_{halogen}} = \frac{20 \text{ V}}{10 \text{ } \Omega} = 2 \text{ A}$.

7. Calculate the current through the unknown resistance R ($I_R$): The current $I_{bulb}$ flows through the series bulb and then splits into $I_{halogen}$ and $I_R$ at the junction before the parallel combination. By Kirchhoff's current law: $I_{bulb} = I_{halogen} + I_R$ $8 \text{ A} = 2 \text{ A} + I_R$ $I_R = 8 \text{ A} - 2 \text{ A} = 6 \text{ A}$.

8. Calculate the value of the unknown resistance R: Using Ohm's law for resistance R: $R = \frac{V_R}{I_R} = \frac{20 \text{ V}}{6 \text{ A}} = \frac{10}{3} \text{ } \Omega$.

The final answer is $\boxed{\frac{10}{3} \Omega}$.

Explanation of the solution:

1. Calculate the resistance of the halogen lamp using its rated power and voltage ($R_{halogen} = V_{rated}^2 / P_{rated}$).
2. Determine the operating voltage across the halogen lamp when its power is 40 W ($V_{halogen} = \sqrt{P_{operating} \times R_{halogen}}$).
3. Since R is parallel to the halogen lamp, the voltage across R is the same as $V_{halogen}$.
4. The 10 $\Omega$ bulb is in series with the parallel combination. The voltage across the 10 $\Omega$ bulb is the total voltage minus the voltage across the parallel combination ($V_{bulb} = V_{total} - V_{halogen}$).
5. Calculate the current through the 10 $\Omega$ bulb ($I_{bulb} = V_{bulb} / R_{bulb}$). This current is the total current entering the parallel combination.
6. Calculate the current through the halogen lamp ($I_{halogen} = V_{halogen} / R_{halogen}$).
7. The current through R is the total current entering the parallel combination minus the current through the halogen lamp ($I_R = I_{bulb} - I_{halogen}$).
8. Finally, calculate R using Ohm's law ($R = V_R / I_R$).

Answer: The value of R is $\frac{10}{3} \Omega$.