Question

A hall has the dimensions $10m\times 12m\times 14m$. A fly starting at one corner ends up at a diagonally opposite corner. What is the magnitude of its displacement?
A) 17m
B) 26m
C) 36m
D) 21m

Answer 1

We need to understand the use of the term ‘displacement’ over distance in this case. We can easily find the body diagonal of the hall given its dimensions, which will serve as the displacement of the fly from one corner to the opposite corner.

Complete answer:
We are given a hall with the dimensions $10m\times 12m\times 14m$. We are told that a fly starts flying from one corner of this room and ends up in the opposite corner. We know that if we are to find the distance travelled by the fly it would be an impossible task. The route taken by the fly should be known to find the exact distance. But here we are just asked to find the displacement of the fly.

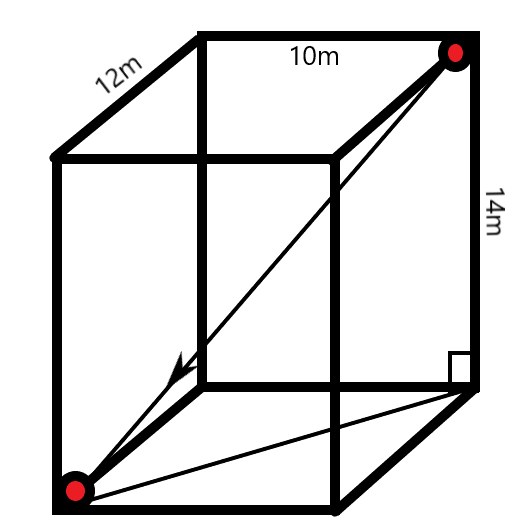
The displacement is the shortest distance between two points. For a hall with the given dimensions, the shortest distance or the displacement between the two opposite corners of the hall will be the body diagonal irrespective of any other parameters.

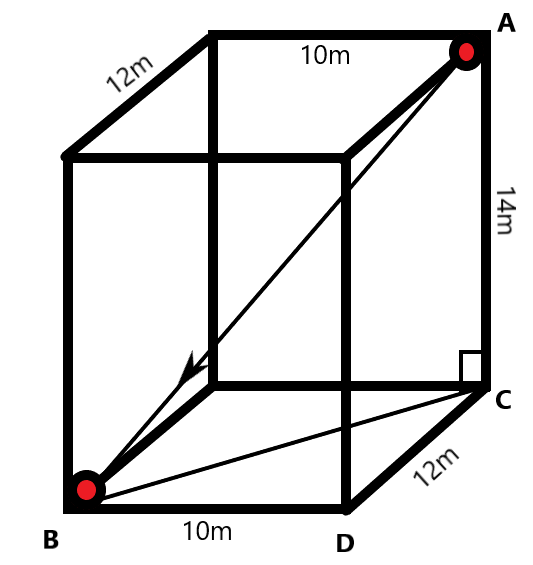
Now, let us consider the situation in which a fly starts from point A and ends in point B. The displacement of the fly is along the line segment AB. We can use the Pythagoras theorem on $\Delta BDC$ as –

& B{{C}^{2}}=B{{D}^{2}}+C{{D}^{2}} \\\ & \Rightarrow BC=\sqrt{B{{D}^{2}}+C{{D}^{2}}} \\\ & \Rightarrow BC=\sqrt{{{10}^{2}}+{{12}^{2}}} \\\ & \therefore BC=2\sqrt{61}m \\\ \end{aligned}$$ Now, again applying Pythagoras theorem in $$\Delta ACB$$, we get – $$\begin{aligned} & A{{B}^{2}}=B{{C}^{2}}+A{{C}^{2}} \\\ & \Rightarrow AB=\sqrt{B{{C}^{2}}+A{{C}^{2}}} \\\ & \Rightarrow AB=\sqrt{{{(2\sqrt{61})}^{2}}+{{14}^{2}}} \\\ & \Rightarrow AB=\sqrt{440}m \\\ & \therefore AB=20.97m\approx 21m \\\ \end{aligned}$$ We get the body diagonal of the hall as 21m. This is the displacement of the fly in the hall. **The correct answer is option D.** **Note:** We have considered the dimensions in its standard order as the length, breadth and height. We assumed that the fly started from the top end corner of the hall and ended at the opposite bottom corner in order to arrive at the solution as above.