Question

A gun with a muzzle velocity of $500ms^{-1}$ shoots a bullet at a bird 50 m away. To hit the bird, the gun should be aimed ($g \ = \ 10ms^{-2}$).
A. Directly towards the bird along the line joining the gun and bird.
B. 10 cm high above the bird.
C. 5 cm high above the bird.
D. 5 cm below the bird.

Answer 1

Whenever there is a force in particular direction acting onto a body, it starts moving in that direction, however small the velocity may be. Whenever a bullet is fired on earth, the gravitational pull of earth pulls the bullet towards the ground. Hence to hit the bird, we have to hit a little bird higher so that it could hit the bird.
Formula used:
$s=ut+\dfrac 12 gt^2, v=\dfrac dt.$

Complete answer:
Since the bird is 50 m away, hence the bullet has to travel the horizontal distance of 50m and there is no force in horizontal direction, hence to find the time taken to hit the bullet, we can directly use $v= \dfrac dt$. Hence $t= \dfrac dv = \dfrac {50}{500} = 0.1s$
Hence the bullet will hit the bullet after 0.1s of firing. Meanwhile the bullet also travels downwards. Thus we shall shift upward by some distance so that bullets don’t miss the bird.
Thus using $s=ut+\dfrac 12 gt^2$ in downward direction, thus $u = 0ms^{-1}, a = -g = -10 ms^{-2}$
Hence $s= 0 + \dfrac 12 {-10}(0.1)^2 = -0.05m = -5cm$
Here, negative signs suggest the movement of the bullet in downward direction.
Hence we have to shift by +5cm or 5cm high to hit the bird.

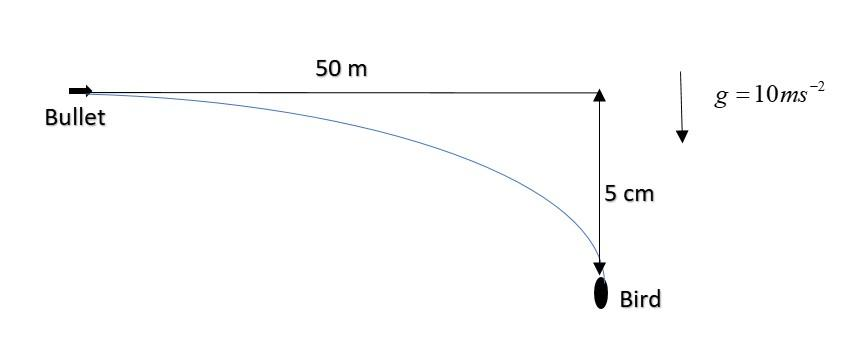
So, the correct answer is “Option C”.

Note:
One should pay attention to the point that we can use the formula $v = \dfrac dt$ only when the acceleration of the particle in the direction is zero. In case it is non zero, we have to use the equations of kinematics to find different parameters. In addition to this, when a particle is released on earth, it can undergo only two types of motion, straight line (when the velocity is along the direction of ‘g’) and parabola (when the velocity is not in the direction of ‘g’).