Question

A gun of mass $'{{m}_{1}}'$ fires a bullet of mass $'{{m}_{2}}'$ with a horizontal speed $'{{v}_{0}}'$. The gun is fitted with a concave mirror of focal length $f$ facing toward a receding bullet. Find the speed of separation of the bullet and the image just after the gun was fired.

& A.\left( 1+\dfrac{{{m}_{2}}}{{{m}_{1}}} \right){{v}_{0}} \\\ & B.2\left( 1-\dfrac{{{m}_{2}}}{{{m}_{1}}} \right){{v}_{0}} \\\ & C.2\left( 1+\dfrac{2{{m}_{2}}}{{{m}_{1}}} \right){{v}_{0}} \\\ & D.2\left( 1+\dfrac{{{m}_{2}}}{{{m}_{1}}} \right){{v}_{0}} \\\ \end{aligned}$$

Answer 1

Here, the gun is fitted on a concave mirror. We will need a diagram for proper understanding. We will use the law of conservation of momentum for the gun and bullet fired from which we will find the mirror speed. Then we will find the speed of the bullet with respect to the mirror which is the same as the speed of the image by adding as we are finding relative velocity.

Formula used:
${{m}_{1}}{{u}_{1}}+{{m}_{2}}{{u}_{2}}={{m}_{1}}{{v}_{1}}+{{m}_{2}}{{v}_{2}}$

Complete step by step answer:
First we will draw a diagram for better understanding.

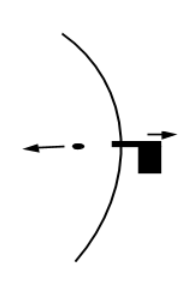
Now, let us take ${{v}_{1}}$ as the velocity of the gun or mirror (both will be the same). Then we are considering the law of conservation of momentum for the gun and bullet.
${{m}_{1}}{{u}_{1}}+{{m}_{2}}{{u}_{2}}={{m}_{1}}{{v}_{1}}+{{m}_{2}}{{v}_{2}}$

But before firing, both will be at rest. So, the equation will change as

& 0={{m}_{1}}{{v}_{1}}-{{m}_{2}}{{v}_{0}} \\\ & {{m}_{1}}{{v}_{1}}={{m}_{2}}{{v}_{0}} \\\ \end{aligned}$$ From this, we can find the velocity if mirror as $${{v}_{1}}=\dfrac{{{m}_{2}}{{v}_{0}}}{{{m}_{1}}}$$. Then the velocity bullet with respect to the mirror will be the relative velocity. i.e. if we take the rate at which the distance between mirror and bullet increasing, it will be $$\dfrac{\delta u}{\delta t}={{v}_{1}}+{{v}_{0}}$$. Here, the bullet is fired at the pole. So there will be no magnification. i.e. $$m=\dfrac{u}{v}=1$$ If we take rate of change in image distance, $$\dfrac{\delta v}{\delta t}=\left( \dfrac{{{v}^{2}}}{{{u}^{2}}} \right)\dfrac{\delta u}{\delta t}$$. But we know magnification is 1. So, $$\dfrac{\delta v}{\delta t}=\dfrac{\delta u}{\delta t}$$ Therefore, $$\dfrac{\delta v}{\delta t}=\dfrac{\delta u}{\delta t}={{v}_{1}}+{{v}_{0}}$$ Now, let us take $$\dfrac{\delta v}{\delta t}$$ as rate at which distance between image and mirror increasing and $${{v}_{2}}$$ as absolute velocity of image. Then, according to relative velocity between mirror and image, $${{v}_{2}}-{{v}_{1}}=\dfrac{\delta v}{\delta t}={{v}_{1}}+{{v}_{0}}$$ $$\Rightarrow {{v}_{2}}=2{{v}_{1}}+{{v}_{0}}$$ Therefore, speed of separation of bullet and image will be $${{v}_{r}}={{v}_{2}}+{{v}_{0}}=2{{v}_{1}}+{{v}_{0}}+{{v}_{0}}$$ $$\Rightarrow {{v}_{r}}=2\left( {{v}_{1}}+{{v}_{0}} \right)$$ If we substitute the value of $${{v}_{1}}$$ which we obtained, we will get $$\begin{aligned} & {{v}_{r}}=2\left( \dfrac{{{m}_{2}}{{v}_{0}}}{{{m}_{1}}}+{{v}_{0}} \right) \\\ & \Rightarrow {{v}_{r}}=2\left( \dfrac{{{m}_{2}}}{{{m}_{1}}}+1 \right){{v}_{0}} \\\ \end{aligned}$$ So we have the speed of separation of the bullet and image as $${{v}_{r}}=2\left( \dfrac{{{m}_{2}}}{{{m}_{1}}}+1 \right){{v}_{0}}$$. Therefore, option d is the right answer. **Note:** We must be very careful while taking the relative velocity because we have two opposing but very similar cases in this. While taking the relative velocity between bullet and mirror, they are travelling in opposite directions, so we will add the velocities. But in the case of an image and mirror they are travelling in the same direction, so we need to take the difference in velocities. Also we must be aware of our frame of reference.