Question

A grating has $350{\text{ rulings/mm}}$ and is illuminated at normal incidence by white light. A spectrum is formed on a screen $30.0{\text{ cm}}$ from the grating. If a hole $10.0{\text{ mm}}$ square is cut in the screen, its inner edge being $50.0{\text{ mm}}$ from the central maximum and parallel to it, what is the
(a) Shortest and
(b) The longest wavelength of the light that passes through the hole?

Answer 1

We are given in diffraction grating with certain rulings which on diffraction through light forms a spectrum at a screen at a certain distance from it. We are required to find the shortest and the longest wavelength that would pass through the slit made in the screen which is parallel to its central maximum.

Complete step by step answer:
Let us draw the diagram to get a clear understanding of the situation given in the question.

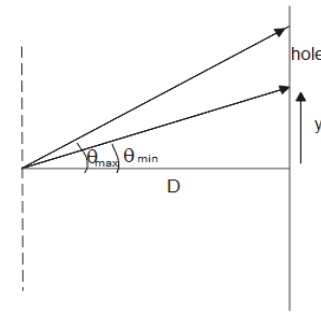
(a) We considered the distance between the diffraction grating and the screen to be $D$ and the distance between the central maximum and inner edge of the hole to be $y$. We can see from the diagram that the minimum angle at the inner edge of the hole can be written as $\tan \theta = \dfrac{y}{D}$
$\Rightarrow {\theta _{\min }} = {\tan ^{ - 1}}\left( {\dfrac{y}{D}} \right)$
Now substituting the given values we get,
$\Rightarrow {\theta _{\min }} = {\tan ^{ - 1}}\left( {\dfrac{{50 \times {{10}^{ - 3}}{\text{m}}}}{{0.300{\text{m}}}}} \right) \\\ \Rightarrow {\theta _{\min }} = 9.46^\circ$

Now the maxima of the diffraction grating are given as
$d\sin \theta = m\lambda$
Where $d = \dfrac{1}{{350{\text{ lines/mm}}}} = \dfrac{1}{{350 \times {{10}^3}}} = 2.86 \times {10^{ - 6}}{\text{ m}}$
And $m$ is the order of diffraction and $\lambda$ is the wavelength of the light used.
Substituting the values for minimum angle we get
$m = \dfrac{{(2.86 \times {{10}^{ - 6}})\sin 9.46^\circ }}{\lambda } \Rightarrow m= \dfrac{{470{\text{ nm}}}}{\lambda }$
Now the allowed order of diffraction is one therefore the shortest wavelength that passes the hole is
$\therefore {\lambda _{\min }} = 470{\text{ nm}}$

(b) Now we can see the maximum angle at the outer edge of the hole in the screen can be written as
${\theta _{\max }} = {\tan ^{ - 1}}\dfrac{{y + 10{\text{ mm}}}}{D}$
We added the length of the hole to the distance between the outer edge and the central maximum.Now substituting the values we get

\Rightarrow {\theta _{\max }} = 11.31^\circ $$ Now again we know $d\sin \theta = m\lambda $ Substituting the values for maximum angle we get $m = \dfrac{{(2.86 \times {{10}^{ - 6}})\sin 11.31^\circ }}{\lambda } \\\ \Rightarrow m= \dfrac{{560{\text{nm}}}}{\lambda }$ We know the allowed value for the order is one therefore the maximum wavelength of light that passes through the hole is $\therefore {\lambda _{\max }} = 560{\text{ nm}}$ **Note:** A diffraction grating consists of a large number of parallel, closely spaced slits which separates light of different wavelengths. The relationship between grating spacing and the angles of diffraction is known as the grating equation which gives us the condition for maxima in a diffraction grating.