Question

A graph between $log t_{1/2}$ and log a, a being initial concentration of A in reaction (A → Products) is given below

Select correct statement(s) based on it.

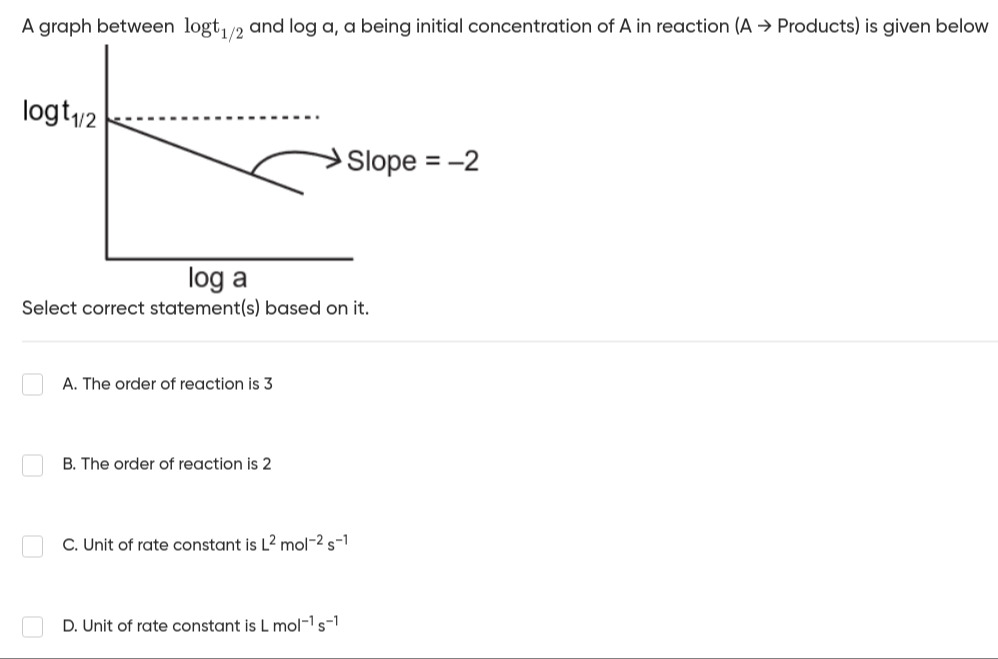
• A. The order of reaction is 3
• B. The order of reaction is 2
• C. Unit of rate constant is $L^2 mol^{-2} s^{-1}$
• D. Unit of rate constant is $L mol^{-1}s^{-1}$

Answer 1

Answer: (A), (C)

A, C

Answer 2

The half-life ($t_{1/2}$) for an n-th order reaction (where $n \neq 1$) is related to the initial concentration ($a$) by the equation: $t_{1/2} = \frac{1}{k(n-1)} \frac{1}{a^{n-1}} = \frac{1}{k(n-1)} a^{1-n}$

Taking the logarithm of both sides: $\log t_{1/2} = \log \left(\frac{1}{k(n-1)}\right) + (1-n) \log a$

This equation is in the form of a straight line, $Y = C + mX$, where: $Y = \log t_{1/2}$ $X = \log a$ The slope of the graph ($m$) is $(1-n)$.

From the given graph, the slope is -2. So, we can write: $1 - n = -2$ $n = 1 - (-2)$ $n = 1 + 2$ $n = 3$

Therefore, the order of the reaction is 3.

Now, let's determine the unit of the rate constant ($k$) for a 3rd order reaction. The general unit of the rate constant for an n-th order reaction is given by: Unit of $k = (\text{concentration})^{1-n} (\text{time})^{-1}$ Using concentration in $\text{mol L}^{-1}$ and time in seconds (s): Unit of $k = (\text{mol L}^{-1})^{1-n} \text{s}^{-1}$

For a 3rd order reaction ($n=3$): Unit of $k = (\text{mol L}^{-1})^{1-3} \text{s}^{-1}$ Unit of $k = (\text{mol L}^{-1})^{-2} \text{s}^{-1}$ Unit of $k = \text{mol}^{-2} \text{L}^{2} \text{s}^{-1}$ This can also be written as $\text{L}^{2} \text{mol}^{-2} \text{s}^{-1}$.

Therefore, statement C is correct.