Question

(a) Good quality sun-glasses made of polaroids are preferred over ordinary colored glasses. Justify your answer.
(b) Two polaroids ${{P}_{1}}$ and ${{P}_{2}}$ are placed in crossed positions. A third Polaroid ${{P}_{3}}$ is kept between ${{P}_{1}}$ and ${{P}_{2}}$ such that pass axis of ${{P}_{3}}$ is parallel to that of ${{P}_{1}}$. How would the intensity of light $\left( {{I}_{2}} \right)$ transmitted through ${{P}_{2}}$ vary as ${{P}_{3}}$ is rotated? Draw a plot of intensity $'{{I}_{2}}'$ Vs the angle $'\theta '$, between pass axes of ${{P}_{1}}$ and ${{P}_{3}}$.

Answer 1

As a first step, you should represent the given condition in a diagram. Now you should make use of Malu’s law to find the intensity of the beam transmitted through the third Polaroid introduced between the other two. Now you should accordingly find the intensity of the beam transmitted through ${{P}_{2}}$ and then make a plot of the variation of the intensity with $\theta$.
Formula used:
Malu’s law,
$I={{I}_{0}}{{\cos }^{2}}\theta$

Complete step-by-step solution
(a) In the question, we are asked to justify why good quality sun-glasses made of polaroids are preferred over ordinary colored glasses.
Polaroid glasses have this advantage over colored glasses in that they have the capability to cut off harmful UV rays of the sun thus providing our eyes better protection. The intensity of light transmitted by Polaroid glasses is also low and also is more effective in reducing the glare due to reflections from horizontal surfaces. Hence, the given statement is justified.
(b) Here, two polaroids are kept in cross position with each other. A third polaroid is introduced in between them and is kept parallel to the first Polaroid. We are asked to find the variation of intensity of light transmitted by ${{P}_{2}}$ when ${{P}_{3}}$ is rotated by angle $\theta$ and also to plot the variation.

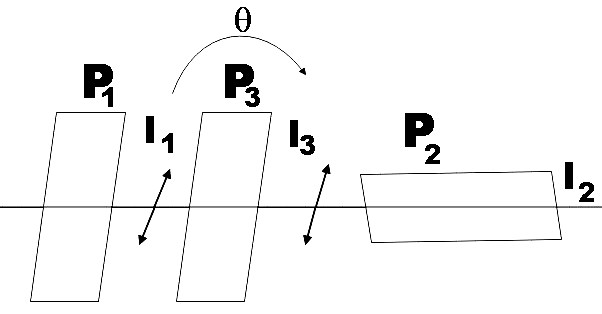
Clearly, the pass axis of ${{P}_{1}}$ and ${{P}_{2}}$ are at $\dfrac{\pi }{2}$ angle with each other. Let $\theta$ be the angle at which ${{P}_{3}}$ is being rotated. So the angle between the pass axis of ${{P}_{2}}$ and ${{P}_{3}}$ will be $\left( \dfrac{\pi }{2}-\theta \right)$.
If the intensity of light coming through ${{P}_{1}}$ is${{I}_{1}}$, then, by malu’s law the intensity of the light passing through ${{P}_{3}}$ will be given by,
${{I}_{3}}={{I}_{1}}{{\cos }^{2}}\theta$ ……………………………. (1)
The intensity of light transmitted through ${{P}_{3}}$ would be,
${{I}_{2}}={{I}_{3}}{{\cos }^{2}}\left( \dfrac{\pi }{2}-\theta \right)$
$\Rightarrow {{I}_{2}}={{I}_{3}}{{\sin }^{2}}\theta$
Substituting (1),
${{I}_{2}}=\left( {{I}_{1}}{{\cos }^{2}}\theta \right){{\sin }^{2}}\theta$
$\therefore {{I}_{2}}={{I}_{1}}\dfrac{{{\left( \sin 2\theta \right)}^{2}}}{4}$
Thus we found the expression for the variation of the intensity of light$\left( {{I}_{2}} \right)$ transmitted through ${{P}_{2}}$ with the angle at which ${{P}_{3}}$ is rotated as,
${{I}_{2}}={{I}_{1}}\dfrac{{{\left( \sin 2\theta \right)}^{2}}}{4}$
Now let us make the plot of this variation,

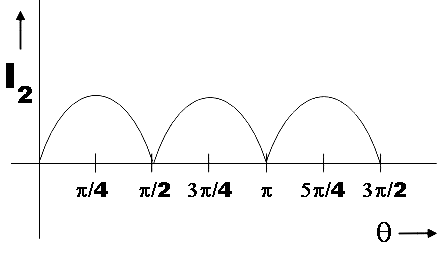
Note: Malu’s law states that the intensity of the plane-polarized light, when passed through a rotatable polarizer, varies as the square of the cosine of the angle at which the polarizer is rotated. We have made the plot by substituting various values for $\theta$ in the above expression and thus finding the variation for ${{I}_{2}}$ with it. As the relation is a function of the square of sine the intensity is found to be positive in the plot.