Solveeit Logo
Login

Question

Question: A glass wind screen whose inclination with the vertical can be changed is mounted on a car. The car ...

A glass wind screen whose inclination with the vertical can be changed is mounted on a car. The car moves horizontally with a speed of 2m s−12m{\text{ }}{s^{ - 1}} . At what angle α\alpha with the vertical should the wind screen be placed so that the rain drops falling vertically downwards with velocity 6m s−16m{\text{ }}{s^{ - 1}} strike the wind screen perpendicularly?
A. tan⁡−1(3){\tan ^{ - 1}}(3)
B. tan⁡−1(4){\tan ^{ - 1}}(4)
C. tan⁡−1(13){\tan ^{ - 1}}\left( {\dfrac{1}{3}} \right)
D. tan⁡−1(14){\tan ^{ - 1}}\left( {\dfrac{1}{4}} \right)

Explanation

Solution

To answer this type of question one must have the concept of relative motion. Here we will make a diagram as given below for an easy solution and then we will use the resultant of both the vectors to get the required solution.

Complete step by step solution:
According to the question,
Speed of the car moving horizontally is, V1=2m s−1{V_1} = 2m{\text{ }}{s^{ - 1}}
Velocity of drops of the rain falling vertically is, V2=6m s−1{V_2} = 6m{\text{ }}{s^{ - 1}}
And we have to find that,
Let us consider this figure,

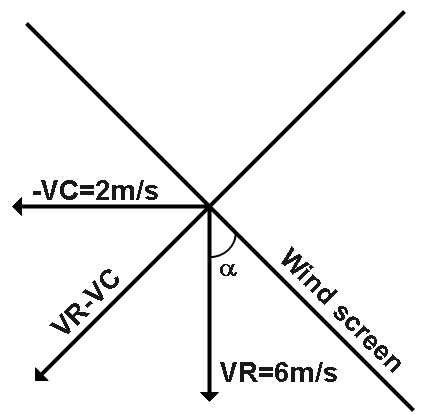
Velocity of rain with respect to car VRC=VR−VC{V_{RC}} = {V_R} - {V_C} should be perpendicular to the wind screen,
i.e., Components of VR{V_R} and −VC - {V_C} parallel to the wind screen should cancel each other,
i.e.,

6cos⁡α=2sin⁡α ⇒tan⁡α=62 ⇒tan⁡α=3 ⇒α=tan⁡−1(3)  6\cos \alpha = 2\sin \alpha \\\ \Rightarrow \tan \alpha = \dfrac{6}{2} \\\ \Rightarrow \tan \alpha = 3 \\\ \Rightarrow \alpha = {\tan ^{ - 1}}(3) \\\

So, the angle α\alpha with the vertical should the wind screen be placed so that the rain drops falling vertically downwards with velocity 6m s−16m{\text{ }}{s^{ - 1}} strike the wind screen perpendicularly is tan⁡−1(3){\tan ^{ - 1}}(3) .
Hence, the correct option is A.

Note:
In this two dimensional way of considering the relative motion velocity, two objects are taken A and B which are moving with the velocity of VA and VB in opposite direction, due to which the negative sign is taken in the value of relative velocity, with respect to the reference frame (ground or earth). There can be two conditions in this type of velocity calculation, which are the velocity of object A with respect to the velocity of object B and the velocity of object A with respect to the velocity of object B.