Question

A glass rod of radius $r_{1}$ is inserted symmetrically into a vertical capillary tube of radius $r_{2}$ such that their lower ends are at the same level. The arrangement is now dipped in water. The height to which water will rise into the tube will be $(\sigma=$ surface tension of the water, $\rho=$ density of water).

& A.\frac{2\sigma }{({{r}_{2}}-{{r}_{1}})\rho g} \\\ & B.\frac{\sigma }{({{r}_{2}}-{{r}_{1}})\rho g} \\\ & C.\frac{2\sigma }{({{r}_{2}}+{{r}_{1}})\rho g} \\\ & D.\frac{2\sigma }{(r_{2}^{2}+r_{1}^{2})\rho g} \\\ \end{aligned}$$

Answer 1

Surface tension is the property of liquid due to the force of attraction of particles on the surface layer, which tends to minimize the surface area. To find the height, we need to find the force due to the surface tension and the weight of the liquid due to height. i.e. $F=[2\sigma \pi r_{1}+2\sigma \pi r_{2}]$and $w=h\pi[ r_{1}^{2}-r_{2}^{2}]\rho g$. We must equate them.

Formula used:
$F=[2\sigma \pi r_{1}+2\sigma \pi r_{2}]$
$w=h\pi[ r_{1}^{2}-r_{2}^{2}]\rho g$

Complete step-by-step answer:
Surface tension is the property of liquid due to the force of attraction of particles on the surface layer, which tends to minimize the surface area. Its dimension is force per unit length. At any point in the medium, there is a force of attraction called the cohesive forces which act in every direction resulting in the net force zero. But at the surface, the molecules are pulled inwards towards the liquid; this causes the surface area of the liquid to minimize. Surfactants are used to minimize the surface tension and hence increase the surface area.

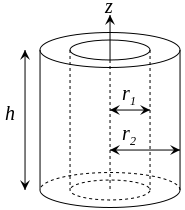
We know that the total upward force due to surface tension $F=[2\sigma \pi r_{1}+2\sigma \pi r_{2}]$
Then the weight of the liquid column of height $h$ is $w=h\pi[ r_{1}^{2}-r_{2}^{2}]\rho g$ where$\rho=$ density.
Then equating the two we get, $F=w$
$2\sigma \pi[r_{1}+r_{2}]=h\pi \rho g[r_{1}^{2}-r_{2}^{2}]$
$h=\dfrac{2\sigma}{\rho g(r_{1}-r_{2})}$
Hence the answer is A.$\dfrac{2\sigma}{(r_{2}-r_{1})\rho g}$

Note: The question might look complicated, at the first sight. But here if we must remember the following equations$F=[2\sigma \pi r_{1}+2\sigma \pi r_{2}]$ and$w=h\pi[ r_{1}^{2}-r_{2}^{2}]\rho g$. And must equate them. We can get the required answer. Also note that the height till which the capillary tube is filled depends on the surface tension and density of the liquid.