Question

A glass plate of refractive index, $1.5$ is coated with a thin layer of thickness $d$ and refractive index $1.8$. Light of wavelength $648\,nm$ travelling in air is incident normally on the layer. It is partly reflected at upper and lower surfaces of the later and the rays interfere constructively is?
A. $30\,nm$
B. $60\,nm$
C. $90\,nm$
D. $120\,nm$

Answer 1

Interference of light is the property of light in which upon superposition of coherent light (of same frequency) the intensity of light becomes maximum or minimum depending on the phase difference between the rays.

Formula used:
For constructive interference of two rays the condition is given by,
$\Delta = n\lambda$
where $\Delta$ is the path difference between the superposed waves, $\lambda$ is the wavelength of the light and $n$ is an integer.

Complete step by step answer:
We have here a glass plate of refractive index $1.5$ which is coated with a thin layer of thickness $d$ and refractive index $1.8$. The passing light is of wavelength is $648\,nm$.Now, the path of the wave can be shown by the following diagram.

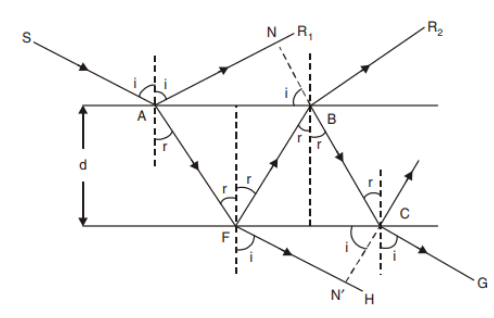
So, from the diagram we can see that, ray $A{R_1}$ and ray $B{R_2}$ will superposed and will form interference patterns in the glass. Now, we have to find the path difference between these two waves upon a normal incident. Now, the path covered by the ray $B{R_2}$ is ${\mu _2}(AF + FB)$ and the path covered by the ray $A{R_1}$ is ${\mu _1}AN$. Now, since the two waves reflect from two different surfaces there will be an extra path difference of $\dfrac{\lambda }{2}$ due to the change of medium twice of the ray $B{R_2}$. Hence, the path difference between the ray $A{R_1}$ and ray $B{R_2}$ will be,
$\Delta = {\mu _2}(AF + FB) - {\mu _1}AN - \dfrac{\lambda }{2}$
$\Rightarrow \Delta = 2{\mu _2}AF - {\mu _1}AN - \dfrac{\lambda }{2}$

Now, from simple trigonometry we can see that,
$AF = \dfrac{d}{{\cos r}}$ and $AN = AB\sin i$
Also, $AB = d\tan r$
So, putting these values we have,
$\Delta = 2{\mu _2}\dfrac{d}{{\cos r}} - {\mu _1}2d\tan r\sin i - \dfrac{\lambda }{2}$
Now, using Snell’s law we can write,
$\Delta = 2{\mu _2}\dfrac{d}{{\cos r}} - {\mu _1}2d\dfrac{{\sin r}}{{\cos r}}\dfrac{{{\mu _2}}}{{{\mu _1}}}\sin r - \dfrac{\lambda }{2}$
$\Rightarrow \Delta = 2{\mu _2}\dfrac{d}{{\cos r}}(1 - {\sin ^2}r) - \dfrac{\lambda }{2}$
$\Rightarrow \Delta = 2{\mu _2}d\cos r - \dfrac{\lambda }{2}$
Now, for constructive interference we know, the path difference is $\Delta = n\lambda$.So, we can write,
$2{\mu _2}d\cos r - \dfrac{\lambda }{2} = m\lambda$
$\Rightarrow 2{\mu _2}d\cos r = m\lambda + \dfrac{\lambda }{2}$

Now, for normal incidence the angle of refraction is ${0^ \circ }$ hence,
$\cos {0^ \circ } = 1$
Therefore,
$2{\mu _2}d = (m + \dfrac{1}{2})\lambda$
Now, putting the value of the refractive index and wavelength for the first order we have,
${d_{\min }} = \dfrac{1}{{4{\mu _2}}}\lambda$
$\Rightarrow {d_{\min }} = \dfrac{1}{{4 \times 1.8}}648\,nm$
$\therefore {d_{\min }} = 90\,nm$
Therefore the rays interfere constructively for the minimum layer thickness of $90nm$

Hence, option C is the correct answer.

Note: The formation of the interference pattern does not depend on the refractive index of the incident medium it only depends on the medium of the film or coat. Remember that when a light rays reflects back from one medium to another medium the phase of the light changes by $\pi$as changing the path difference of the wave by $\dfrac{\lambda }{2}$ factor.