Solveeit Logo
Login

Question

Question: A glass capillary tube is of the shape of truncated cone with an apex angle \(\alpha \) so that its ...

A glass capillary tube is of the shape of truncated cone with an apex angle α\alpha so that its two ends have cross sections of different radii. When dipped in water vertically, water rises in it to a height h, where the radius of its cross section if b. if the surface tension of water is S, its density is ρ\rho , and its contact angle with glass is θ\theta , the value of h will be (g is the acceleration due to gravity)
A. 2Sbgρcos⁡(θ−α)\dfrac{2S}{bg\rho }\cos (\theta -\alpha )
B. 2Sbgρcos⁡(θ+α)\dfrac{2S}{bg\rho }\cos (\theta +\alpha )
C. 2Sbgρcos⁡(θ−α2)\dfrac{2S}{bg\rho }\cos (\theta -\dfrac{\alpha }{2})
D. 2Sbgρcos⁡(θ+α2)\dfrac{2S}{bg\rho }\cos (\theta +\dfrac{\alpha }{2})

Explanation

Solution

Hint: Use the concept of capillary action and angle of contact. Surface tension for liquid makes liquid to have a minimum possible area. Draw geometry over capillary. Use triangle property and rearrange or adjust the equation to get the result.

Complete step by step solution:

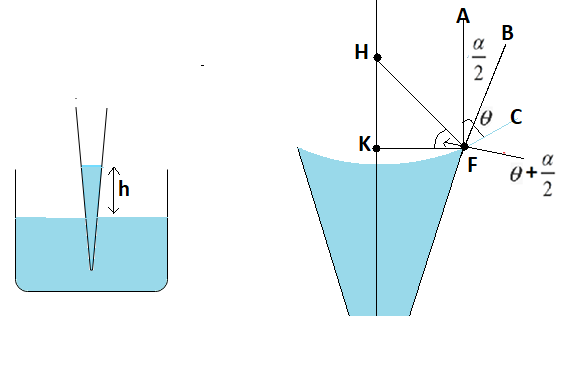
FA= extension of curved portion of capillary
FB= extension of edges of capillary tube
FA= perpendicular drawn
FH= line joining the point F with capillary axis at point H
FK= line joining the point F with capillary axis at point K

∠KFH=θ+α2\angle KFH=\theta +\dfrac{\alpha }{2}
∠CFB=θ\angle CFB=\theta
∠AFB=α2\angle AFB=\dfrac{\alpha }{2}

When a glass of fine bore is dipped in a liquid, the liquid rises immediately to a certain height due to surface tension. The liquid column exerts a force by S per unit length of a line of contact at an inclination θ\theta with the vertical and R is the radius of a capillary tube.

InΔFKH cos⁡(θ+α2)=bR \begin{aligned} & In\Delta FKH \\\ & \cos (\theta +\dfrac{\alpha }{2})=\dfrac{b}{R} \\\ \end{aligned}

Applying surface tension to capillary, we get
P0−2SR+hgρ=P0 hgρ=2SR \begin{aligned} & {{P}_{0}}-\dfrac{2S}{R}+hg\rho ={{P}_{0}} \\\ & hg\rho =\dfrac{2S}{R} \\\ \end{aligned}
Where, R=radius of capillary tube

h=2SRgρh=\dfrac{2S}{Rg\rho }

Put value of R, then
h=2Sgbρcos⁡(θ+α2)h=\dfrac{2S}{gb\rho }\cos (\theta +\dfrac{\alpha }{2})

So the correct option is D.

Additional information:
Angle of contact θ\theta is the angle made by tangent at the point of contact of the liquid surface with solid surface inside the liquid. The angle of contact is acute i.e. less than 90 for Water and angle of contact is obtuse i.e. more than 90 for mercury.

Note: Concept of capillary action is the same of all kinds of shape whether it is cone square or anything. You just need to take care of the cross-section of the capillary tube, a radius of it and water rise at a certain height. Don’t get confused about the shape of capillary tubes.