Question

A given right circular cone has a volume p, and the largest right circular cylinder that can be inscribed in the cone has a volume q. Then p : q is –

• A. 9 : 4
• B. 8 : 3
• C. 7 : 2
• D. ) None of these

Answer 1

Answer: (A)

9 : 4

Answer 2

Let H be the height of the cone and a be its semi vertical angle. Suppose that x is the radius of the inscribed cylinder and h be its height

h = QL = OL – OQ = H – x cot a

V = volume of the cylinder = px² (H – x cot a)

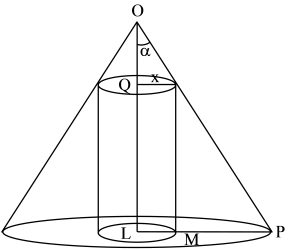
Also p = $\frac { 1 } { 3 }$ p (H tan a)² H (i)

= p (2Hx – 3x² cot a)

So $\frac { \mathrm { dV } } { \mathrm { dx } }$ = 0 Ū x = 0, x = $\frac { 2 } { 3 }$ H tan a

= – 2ph < 0.

So V is maximum when x = $\frac { 2 } { 3 }$H tan a and

q = V_max = $\frac { 4 } { 9 }$ H² tan² a $\frac { 1 } { 3 }$H

= $\frac { 4 } { 9 }$ p. [using (i)]

Hence p : q = 9 : 4.