Question

A given object takes $n$ times more time to slide down a $45^{\circ}$ rough inclined plane as it takes to slide down a perfectly smooth $45^{\circ}$ incline. The coefficient of kinetic friction between the object and the incline is :

• A. $\frac{1}{1 -n^2}$
• B. $1 - \frac{1}{n^2}$
• C. $\sqrt{ 1 - \frac{1}{n^2}}$
• D. $\sqrt{\frac{1}{1 - n^2}}$

Answer 1

Answer: (B)

$1 - \frac{1}{n^2}$

Answer 2

Consider the following figures:

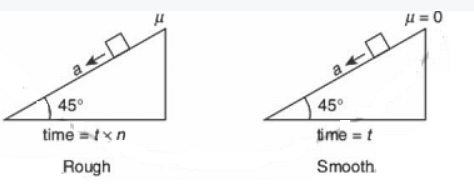
We know that for a body moving with constant acceleration, the kinematics equation is given as $s=u t+\frac{1}{2} a t^{2}$.
Initial velocity, $u=0 \Rightarrow s=\frac{1}{2} a t^{2}$
$\Rightarrow 2 s=a t^{2}$
$\Rightarrow t=\sqrt{\frac{2 s}{a}}$
$\Rightarrow t \propto \frac{1}{\sqrt{a}}$
Now for smooth inclined plane $a_{s}=g \sin \theta$
For rough inclined plane $a_{ r }=g \sin \theta-g \mu \cos \theta$
Also, time taken to travel down the smooth inclined plane $t_{ s }=t$ and time taken to travel down the rough inclined plane $t_{r}=n t .$
Therefore, $\frac{t_{s}}{t_{r}} =\sqrt{\frac{a_{t}}{a_{s}}}$
$\Rightarrow \frac{t_{s}^{2}}{t_{r}^{2}}=\frac{a_{t}}{a_{s}}$
$\Rightarrow \frac{t_{s}^{2}}{t_{r}^{2}}=\frac{g \sin \theta-g \mu \cos \theta}{g \sin \theta}=1-\mu \tan \theta$
$\Rightarrow \frac{t^{2}}{n^{2} t^{2}} =1-\mu \tan \theta$
$\Rightarrow \frac{1}{n^{2}}=1-\mu \tan \theta$
$\Rightarrow \mu \tan \theta=1-\frac{1}{n^{2}}$
$\Rightarrow \mu=\left(1-\frac{1}{n^{2}}\right) \tan \theta$
Now we know $\theta=45^{\circ} \Rightarrow \tan 45^{\circ}=1$
Therefore,
$\mu=1-\frac{1}{n^{2}}$