Question

A girl walks 4km towards west, then she walks 3km in the direction of 30 east of north and stops. Determine the girl's displacement from her initial point of departure.

Answer 1

Hint:Assume that the girl starts from the origin. Take east as the positive direction of the x-axis, west as the negative direction of the x-axis, north as the positive direction of the y-axis and south as the negative direction of the y-axis. Find the coordinates of the final position in this coordinate system and find the net displacement using the distance formula. Alternatively, write each displacement vector in $\mathbf{i}$ and $\mathbf{j}$ vectors and then find the net displacement vector. Take modulus to find the magnitude of the net displacement.

Complete step-by-step answer:
Let the girl start from origin O. The east, west, north and south directions are taken as shown in the diagram.

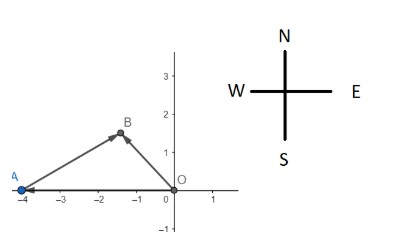
Let A be the position of the girl when she moves 4 km in west direction and B the position of the girl when she moves 3km in 30 east of north direction as shown in the diagram above.
Hence the coordinates of A are (-4,0)
We know that the slope of the line is given by $\tan\theta$ where $\theta$ is an inclination of angle made by line with x-axis .
Here $\theta$ is $30{}^\circ$ then the slope of the line AB is $\tan 30{}^\circ =\dfrac{1}{\sqrt{3}}$
We know by the parametric form of the equation of a line if a point A on a line is at a distance of r from another point $B\left( {{x}_{1}},{{y}_{1}} \right)$ from the line, then the coordinates of A are given by $A\equiv \left( {{x}_{1}}+r\cos \theta ,{{y}_{1}}+r\sin \theta \right)$, where $\theta$ is the angle between the vector BA and the positive direction of the x-axis
Hence by the parametric form of the equation of a line, the equation of line AB is
$\left( -4+r\cos 30{}^\circ ,0+r\sin 30{}^\circ \right)=\left( -4+\dfrac{r\sqrt{3}}{2},\dfrac{r}{2} \right)$, where r is a parameter(the distance of a point on the line above the x-axis from A).
Now, we have for point B, r=3
We know distance between two points is given by formula $\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}$
Hence, we have
$B\equiv \left( -4+\dfrac{3\sqrt{3}}{2},\dfrac{3}{2} \right)$
Hence, we have $OB=\sqrt{{{\left( -4+\dfrac{3\sqrt{3}}{2} \right)}^{2}}+{{\left( \dfrac{3}{2} \right)}^{2}}}=\sqrt{16+\dfrac{27}{4}-12\sqrt{3}+\dfrac{9}{4}}=\sqrt{\dfrac{64+27+9-48\sqrt{3}}{4}}$
Hence, we have
$OB=\sqrt{\dfrac{100-48\sqrt{3}}{4}}=\sqrt{25-12\sqrt{3}}$, which is the magnitude of the net displacement.
Also, the direction of the net displacement is ${{\tan }^{-1}}\left( \dfrac{-4+\dfrac{3\sqrt{3}}{2}}{\dfrac{3}{2}} \right)={{\tan }^{-1}}\dfrac{-8+3\sqrt{3}}{3}$

Note: Alternative solution:
We have $\mathbf{OA}=-4\mathbf{i}$
We know that if a vector of magnitude r makes an angle of $\theta$ with the positive direction of the x-axis, then the vector is given by $r\cos \theta \mathbf{i}+r\sin \theta \mathbf{j}$.
Hence, we have
$\mathbf{AB}=\left( 3 \right)\cos 30{}^\circ \mathbf{i}+3\sin 30{}^\circ \mathbf{j}=\dfrac{3\sqrt{3}}{2}\mathbf{i}+\dfrac{3}{2}\mathbf{j}$
Now from triangle law of vector addition, we have
$\mathbf{OB}=\mathbf{OA}+\mathbf{AB}=-4\mathbf{i}+\dfrac{3\sqrt{3}}{2}\mathbf{i}+\dfrac{3}{2}\mathbf{j}=\left( -4+\dfrac{3\sqrt{3}}{2} \right)\mathbf{i}+\dfrac{3}{2}\mathbf{j}$
We know that the magnitude of the vector $\mathbf{v}=a\mathbf{i}+b\mathbf{j}$ is given by $r=\sqrt{{{a}^{2}}+{{b}^{2}}}$ and the angle made by the vector with the positive direction of the x-axis is given by $\phi ={{\tan }^{-1}}\dfrac{b}{a}$.
Hence the magnitude of the displacement OB $=\sqrt{{{\left( -4+\dfrac{3\sqrt{3}}{2} \right)}^{2}}+{{\left( \dfrac{3}{2} \right)}^{2}}}=\sqrt{25-12\sqrt{3}}$ and the direction of the net displacement OB $={{\tan }^{-1}}\dfrac{-8+3\sqrt{3}}{3}$ radians North of East.