Question

A girl walks $4$ kms towards west, and then she walks $3$kms in a direction ${30^\circ }$ east of north and stops. Determine the girl’s displacement from her initial point of departure.

Answer 1

We have given the initial position and final position of the girl. In this problem, a girl starts to walk towards west for some kilometers and then she walks in the direction of east or west and she stops. We are asked to find the displacement of the girl.

Complete step-by-step answer:
Let O is the original position of the girl positive Y-axis north, negative Y-axis south, positive X-axis east and negative Y-axis west. At first, girl starts to move $4$ kms from O to west that is she moves in a negative X-axis and she reaches the point A. Now from the point A she walks $3$ kms in a direction ${30^\circ }$ east of north. Now the dotted line represents the north.

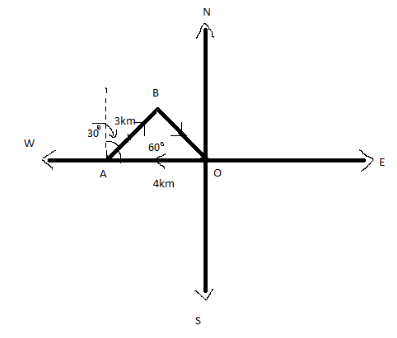
Now we have to find the vector OB.
$\overrightarrow {OA} = \overrightarrow { - 4i}$ Where the minus sign represents that the girl moves in a negative direction and $4$ is the magnitude.
$\overrightarrow {AB} = 3\left( {\cos {{60}^\circ }\overrightarrow i + \sin {{60}^\circ }\overrightarrow j } \right)$
Now substitute the values for $\cos {60^\circ }$ and $\sin {60^\circ }$, we get
$\overrightarrow {AB} = 3 \times \dfrac{1}{2}\overrightarrow i + 3 \times \dfrac{{\sqrt 3 }}{2}\overrightarrow j$
By the triangle law of vector addition, we have
$\overrightarrow {OB} = \overrightarrow {OA} + \overrightarrow {AB}$
Substituting the values,
$( - 4\overrightarrow {i)} + \left( {\dfrac{3}{2}\overrightarrow i + \dfrac{{3\sqrt 3 }}{2}\overrightarrow j } \right)$
Now separate the i vectors and j vectors, we get
$\Rightarrow \left( { - 4 + \dfrac{3}{2}} \right)\overrightarrow i + \dfrac{{3\sqrt 3 }}{2}\overrightarrow j$
Taking LCM, we get
$\Rightarrow \left( {\dfrac{{ - 8 + 3}}{2}} \right)\overrightarrow i + \dfrac{{3\sqrt 3 }}{2}\overrightarrow j$
Hence,
$\Rightarrow \dfrac{{ - 5}}{2}\overrightarrow i + \dfrac{{3\sqrt 3 }}{2}\overrightarrow j$

$\therefore$ The girl’s displacement from her initial point of departure is $\dfrac{{ - 5}}{2}\overrightarrow i + \dfrac{{3\sqrt 3 }}{2}\overrightarrow j$.

Note: In this problem, the values are considered as the vector values, that is the values have both direction and magnitude. Also the answer we have obtained is a vector value where the minus sign represents the negative direction. And also we used the triangle law of vector addition to make the problem easy and solvable.