Question

A girl riding a bicycle with a speed of 5 m/s towards north direction, observes rain falling vertically down. If she increases her speed to 10 m/s, rain appears to meet her at 45° to the vertical. What is the speed of the rain? In what direction does rain fall as observed by a ground based observer?

Answer 1

Hint : Assume north to be $i$ direction and vertically downwards to $- j$ . Let the rain velocity ${v_r}$ be $ai + bj$ . The velocity of the rain observed by the girl is always ${v_r} - {v_g}$ . Draw vector diagrams for the information given and find $a$ and $b$ . We may draw all vectors in the reference frame of the ground-based observer.

Complete Step By Step Answer:
We will separately calculate for both the given cases.
Case-1:
It is given that the velocity of the girl ${v_g} = 5m/s$ .
We can calculate the velocity of the rain with respect to the girl ${v_{rg}}$ by using the formula.
${v_{rg}} = {v_r} - {v_g}$

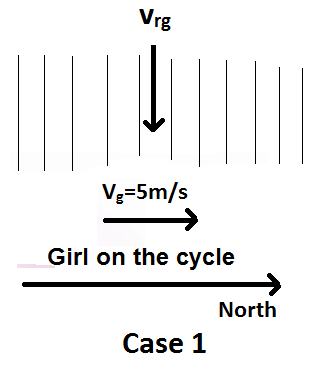
Let the rain velocity ${v_r}$ be $ai + bj$ .
$\Rightarrow {v_{rg}} = ai + bj - 5i = \left( {a - 5} \right)i + bj$
But, it is given that rain is falling vertically down and therefore, its horizontal component will be zero.
$\Rightarrow a - 5 = 0 \\\ \Rightarrow a = 5 \\\$
Case-2:
Now, the girl increases her speed to 10 m/s and the rain appears to meet her at 45° to the vertical as shown in the diagram.

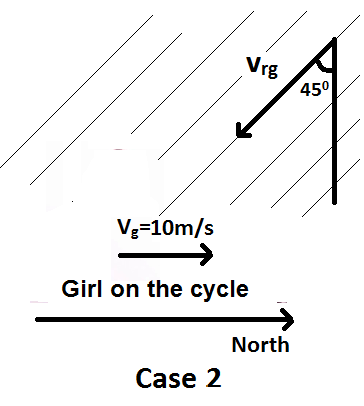
In this case, the velocity of rain with respect to girl is given by:
${v_{rg}} = {v_r} - {v_g} = ai + bj - 10i = \left( {a - 10} \right)i + bj$
As the rain appears to meet the girl at 45° to the vertical as shown in the diagram, we can say that
$\tan {45^ \circ } = \dfrac{b}{{a - 10}}$
We know that $\tan {45^ \circ } = 1$ and $a = 5$ as determined in the first case.
$\dfrac{b}{{5 - 10}} = 1 \\\ \Rightarrow b = - 5 \\\$
Now we have both the values of $a$ and $b$ .
Therefore the velocity of rain $ai + bj$ is:
${v_r} = 5i - 5j$
And the speed of rain will be:
$\left| {{v_r}} \right| = \sqrt {{{\left( 5 \right)}^2} + {{\left( { - 5} \right)}^2}} = \sqrt {50} = 5\sqrt 2 m/s$

Note :
In this question, we have used the concept of relative velocity. Let us consider two objects M and N moving with velocities ${v_M}$ and ${v_N}$ respectively with respect to a common stationary frame of reference.
Then, the relative velocity of object M with respect to object N is given as ${v_{MN}} = {v_M} - {v_N}$ .