Question
Question: A girl of height 150 cm stands in front of a lamp–post and casts a shadow of length \[150\sqrt{3}\] ...
A girl of height 150 cm stands in front of a lamp–post and casts a shadow of length 1503 cm on the ground. Find the angle of elevation of the top of the lamp–post.
Solution
Hint: The formula for writing tangent of an angle is
tanθ=BasePerpendicular .
In this question, we will first draw the figure and mention the respective heights and distances and then we will try to find the angle of elevation of the top of the lamp-post by using the tangent formula in the hence formed triangle.
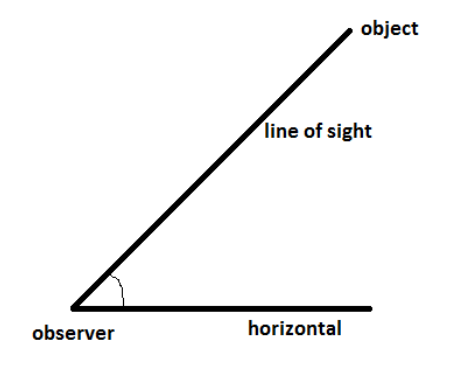
Also, it is important to know what an angle of elevation is
Angle of elevation is the angle that the line of sight makes with the horizontal when we take the observer into consideration.
Complete step-by-step answer:
As mentioned in the question, the figure would look like the below picture
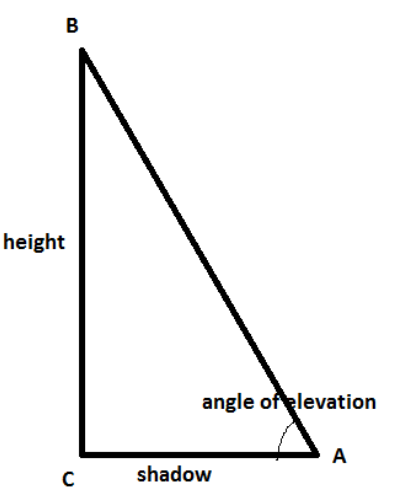
By inspecting the figure, we have
The height of lamp-post BC which is given in the question is given as
=150 cm
And it is also given that the length of the shadow casted by the lamp-post is 1503 cm.
Now, on applying the tangent formula in the ΔABC , we get the angle of elevation of the lamp-post’s top as follows
& \Rightarrow \tan \theta =\dfrac{Perpendicular}{\text{Base}} \\\ & \Rightarrow \tan \theta =\dfrac{150}{\text{150}\sqrt{3}} \\\ & \Rightarrow \tan \theta =\dfrac{1}{\sqrt{3}} \\\ \end{aligned}$$ Now, we know that the value of tan function is $$\dfrac{1}{\sqrt{3}}$$ when the value of $$\theta $$ is $${{30}^{\circ }}$$ , hence, the value of the angle of elevation of the lamp-post’s top is $${{30}^{\circ }}$$. Note: The figure in this question is very tricky and is difficult to visualize it at first. Hence, the students can make an error while drawing the figure and then end up making a mistake and they would get to the correct solution. It is also very essential to know the value of tan function for various common values of $$\theta $$ because without knowing them, one could never get to the correct answer.