Question

A girl of height $1.8m$ is walking away from the base of a lamp post at a speed of $1.2m{s^{ - 1}}$. If the lamp is $4.5m$ above the ground, find the length of her shadow after $5$ seconds.

Answer 1

First we have to calculate the distance of the girl from the lamp post after $5$ seconds. Then express the given data in a figure. Then applying the properties of right-angled triangles and trigonometric equations, we get the desired result.

Useful formula:
If the speed of a body is $x$ metre per second, then the distance covered by the body in $t$ seconds is speed $\times$ time $= xt$.
In a right angled triangle $ABC$ with ${90^ \circ }$ at $A$ and one of the non-right angles, say $\angle B = \theta$ , then $\tan \theta = \dfrac{{AC}}{{AB}}(\dfrac{{{\text{Opposite}}}}{{adjacent}})$

Complete step by step solution:
Given, the height of the girl is $1.8m$.
The speed of the girl is $1.2m{s^{ - 1}}$.
Height of the lamp is $4.5m$.
We have to find the length of her shadow after $5$ seconds.
Consider the figure.

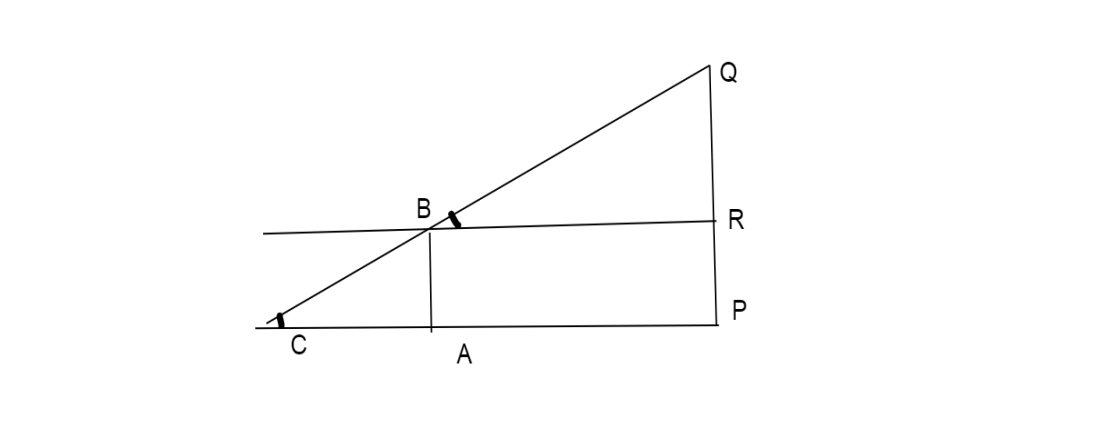
Let $PQ$ represent the lamp post, $PQ = 4.5m$.
$A$ represents the position of the girl after $5$ seconds.
$\Rightarrow AB = 1.8m$
It is given that the girl travels at a speed of $1.2m{s^{ - 1}}$.
Distance covered by her is speed $\times$ time.
Means she covers $1.2 \times 5 = 6m$ in $5$ seconds.
This gives $AP = 6m$.
Draw a line parallel to $AP$ passing through $B$.
Join $BQ$ and extend to meet the line $AP$ at $C$.
Then since $CP$ parallel to $BR$ and $CQ$ is a common line intersecting these lines we have,
$\angle C = \angle B = \theta$
Consider $\vartriangle BRQ$, $BR = AP = 6m$ ( since $AB = PR$)
$\therefore \tan \theta = \dfrac{{{\text{Opposite}}}}{{{\text{adjacent}}}} = \dfrac{{QR}}{{BR}} = \dfrac{{2.7}}{6} - - - (i)$
Now consider $\Delta CAB$, here $AB = 1.8m$
$\therefore \tan \theta = \dfrac{{{\text{Opposite}}}}{{{\text{adjacent}}}} = \dfrac{{AB}}{{AC}} = \dfrac{{1.8}}{{AC}} - - - (ii)$
According to the figure $AC$ is the shadow of the girl after $5$ seconds.
From $(i)$ and $(ii)$ we have, $\dfrac{{2.7}}{6} = \dfrac{{1.8}}{{AC}}$
$\Rightarrow AC = \dfrac{{(1.8) \times 6}}{{2.7}} = \dfrac{{2 \times 6}}{3} = 4$.

Therefore, the length of the shadow of the girl after $5$ seconds is $4m$.

Additional information:
In a right-angled triangle with one of the non-right angles $\theta$, then,
$\sin \theta = \dfrac{{{\text{Opposite}}}}{{{\text{Hypotenuse}}}}$
$\cos \theta = \dfrac{{{\text{Adjacent}}}}{{{\text{Hypotenuse}}}}$
$\tan \theta = \dfrac{{{\text{Opposite}}}}{{{\text{adjacent}}}}$

Note: While solving these kinds of problems one should be careful about the units of the measurements. The speed might be given in kilometres per hour instead of metres per second. In those cases, appropriate conversion must be done before solving.