Question

A girl is in standing position in an oscillating swing. If the girl sits in the swing, the frequency of oscillation
A. Increases
B. Decreases
C. Does not change
D. Becomes zero

Answer 1

The pendulum suspended from a point follows the simple harmonic motion. The simple harmonic motion is defined as a type of periodic motion where the restoring force on the moving object is directly proportional to the object's displacement magnitude and acts towards the object's equilibrium position.

Complete step-by-step answer:
When a girl is on an oscillating swing, this whole setup can be considered to be a simple pendulum. The whole system of the girl oscillating in the swing can be considered as a simple pendulum with point mass where the entire mass of the swing and girl can be assumed to be concentrated at the girl’s centre of gravity and length of the pendulum is the distance between the hinge point of the swing and the centre of gravity.
Here is the pendulum

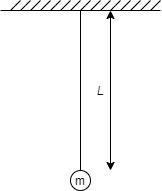
In this pendulum, the mass m represents the total mass concentrated at the centre of gravity and L is the length of the centre of gravity from the hinge.
The time period, or the time taken for one complete oscillation of the simple pendulum is given by –
$T = 2\pi \sqrt {\dfrac{L}{g}}$
where g = acceleration due to gravity.
From this relation, we get –
$T \propto \sqrt L$
This means that the time is directly proportional to the length.
Now, when the girl stands up, the centre of gravity undergoes a shift. The centre of gravity shifts upward and as a result of this, the length L decreases, since the length L is the distance between the support and the centre of gravity.
Thus, the length of the pendulum L, decreases.
Since, the time period is directly proportional to length, the time period decreases.
Frequency of oscillation is defined as the number of oscillations taking place in unit time or 1 second. Frequency is the inverse of time period.
$f = \dfrac{1}{T} \to f \propto \dfrac{1}{T}$
As we know that time period decreases in this case, the frequency increases since they are inversely proportional to each other.

Hence, the correct option is Option A.

Note: In order for a periodic motion to classify as a simple harmonic motion, we have seen that it has to fulfil the basic condition that:
Restoring force, $F \propto - x$ where x is the displacement at every instant.