Question

A girl is 13 m away from a tree. An apple falls from the tree at a height of 2.8 m. If she wants to catch the apple before it hits the ground then how fast does she need to run?
A) 9.83 $m{s^{ - 1}}$
B) 0.75 $\dfrac{m}{s}$
C) More information needed to solve
D) 17.22 $m{s^{ - 1}}$
E) 1.33 $\dfrac{m}{s}$

Answer 1

We can calculate the time that apple will take to fall from the tree using the suitable equation of motion and then the speed using its formula:
$speed = \dfrac{{distance(d)}}{{time(t)}}$
The equation of motion that can be used here is:
$s = ut + \dfrac{1}{2}a{t^2}$
where,
s = Distance
u = Initial velocity
t = Time
a = Acceleration

Complete step by step answer:
According to the question:

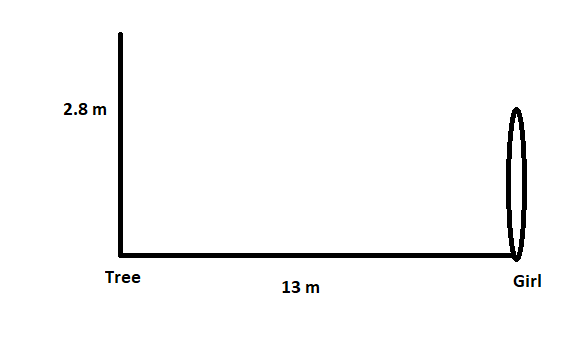
Height of the tree (h) = 2.8 m
Distance of girl from the tree (d) = 13 m
Now, the apple is falling from the tree, the time it will take to fall can be given using equation of motion:
$s = ut + \dfrac{1}{2}a{t^2}$
Here,
u = 0 (as the apple is at rest initially)
s = h (distance will be the height of the tree from where the apple is dropping)
a = g (as the force on the falling apple is gravitational, it will have acceleration due to gravity as its acceleration)
The equation now becomes,
$h = ut + \dfrac{1}{2}g{t^2}$
$h = 0 \times t + \dfrac{1}{2}g{t^2}$ (As u = 0)
$h = \dfrac{1}{2}g{t^2}$
Calculating for t:
${t^2} = \dfrac{{2h}}{g} \\\ t = \sqrt {\left( {\dfrac{{2h}}{g}} \right)} \\\$
Substituting the known values:
$t = \sqrt {\left( {\dfrac{{2h}}{g}} \right)} \\\ t = \sqrt {\left( {\dfrac{{2 \times 2.8}}{{9.8}}} \right)} \\\ t = 0.76s \\\$
Thus the apple will fall down in 0.76 seconds. The speed with she should run:
$speed = \dfrac{{distance(d)}}{{time(t)}}$
Substituting the values, we get:
Speed = $\dfrac{{13}}{{0.76}}$
Speed = 17.11 $m{s^{ - 1}}$ which is approximately equal to 17.22 $m{s^{ - 1}}$
Therefore, if she wants to catch the apple before it hits the ground she needs to run at the speed of approximately 17.22 $m{s^{ - 1}}$ and thus the correct option is D).

Note: This problem was of a falling body (projectile) where g is taken negative or positive according to the direction of the object. It is positive when it is in the direction of motion of the object and negative when in the opposite direction.
Here, the apple was falling downwards and acceleration due to gravity (g) also acts in the downward direction, and hence the g was taken as positive.