Question

A gas park in two processes in which it is heated from the same initial state 1 to the same final temperature. The processes are shown on the P – V diagram by the straight lines 1 – 3 and 1 – 2. 2 and 3 are the points on the same isothermal curve, ${Q_1}$ and ${Q_2}$ are the heat transfer along the two processes. Then –

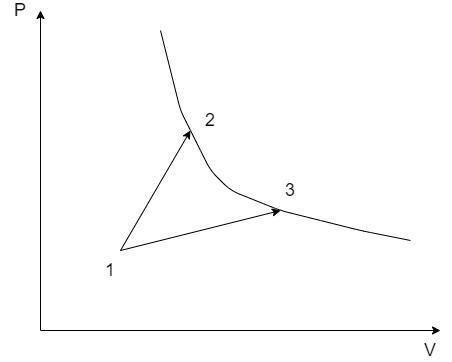
A. ${Q_1} = {Q_2}$
B. ${Q_1} < {Q_2}$
C. ${Q_1} > {Q_2}$
D. Insufficient data

Answer 1

To calculate the heat transferred in both the process, it is important to know the change in the internal energy and change in the work done. Once, those quantities are known, they can be used to calculate the heat energy with the help of the first law of thermodynamics, which gives us the expression.
$Q = \Delta U + W$
which means that the heat energy change in the system is the sum of the change in the internal energy, $\Delta U$ and the work done, W.

Complete step-by-step answer:
Consider the following thermodynamic processes on a P-V diagram:

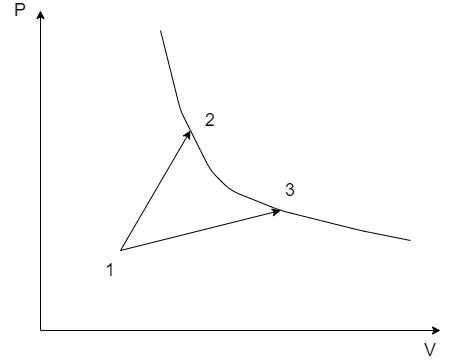
The thermodynamic properties at the states 1, 2 and 3 are denoted by their suffixes such as at state 1, the state properties are ${P_1},{V_1}\& {T_1}$ . The same applies for the states 2 and 3 on the PV graph.
Here, there are two thermodynamic processes 1 – 2 and 1 – 3. Let the heat exchange in the process 1 – 2 be ${Q_1}$ and that of the process 1 – 3 be ${Q_2}$.
The first law of thermodynamics gives us the expression for the heat exchange in a process as:
$Q = \Delta U + W$
which means that the heat energy change in the system is the sum of the change in the internal energy, $\Delta U$ and the work done, W.
First, we have to calculate the change in the internal energy in these processes.
$\Delta {U_1} = n{C_v}\Delta T = n{C_v}\left( {{T_2} - {T_1}} \right)$
$\Delta {U_2} = n{C_v}\Delta T = n{C_v}\left( {{T_3} - {T_1}} \right)$
where n is the number of moles of the gas and ${C_v}$ is the specific heat at constant volume.
Since points 2 and 3 are on an isotherm, ${T_2} = {T_3}$
Thus, $\Delta {U_1} = \Delta {U_2} = 0$
The isothermal work done, is given by the formula,
$W = nRT\ln \left( {\dfrac{{{V_2}}}{{{V_1}}}} \right)$
Now, the work done in the process 1 – 2: ${W_1} = nRT\ln \left( {\dfrac{{{V_2}}}{{{V_1}}}} \right)$
The work done in the process 1 – 3: ${W_2} = nRT\ln \left( {\dfrac{{{V_3}}}{{{V_1}}}} \right)$
From the PV graph, since the volume ${V_3} > {V_2} \Rightarrow {W_2} > {W_1}$
Now that we have the work and internal energy changes in both the process, applying the first law of thermodynamics to these processes, we have –
${Q_1} = \Delta U + {W_1}$
${Q_2} = \Delta U + {W_2}$
Subtracting them, we have –
${Q_2} - {Q_1} = {W_2} - {W_1} + 0 - 0$
$\Rightarrow {Q_2} - {Q_1} = {W_2} - {W_1}$
Since, ${W_2} > {W_1} \Rightarrow {Q_2} > {Q_1}$
Or ${Q_1} < {Q_2}$

Hence, the correct option is Option B.

Note: The students should understand in an isothermal process, we have shown that the change in the internal energy is zero and hence, the heat energy supplied to the system can be directly converted to the work done. Hence, this is the most efficient process but, achieving the heat transfer at an isothermal process is a very big challenge in real-life conditions.